Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số y = m x - 2 x - m + 1 tiếp xúc với parabol y = x 2 + 7
A. m = 7
B. m = 7
C. m = 4
D. với mọi m ∈ ℝ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 12 2018
Đáp án B
Để 
có tiệm cận ngang thì
Khi đó phương trình đường tiệm cận ngang là 
d tiếp xúc với parabol 
CM
3 tháng 6 2018
Điều kiện:mx2+1>0.
- Nếu m=0 thì hàm số trở thành y=x+1 không có tiệm cận ngang.
- Nếu m<0 thì hàm số xác định ⇔ - 1 - m < x < 1 - m
Do đó, lim x → ± ∞ y không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Nếu m>0 hì hàm số xác định với mọi x.
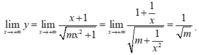
Suy ra đường thẳng y = 1 m là tiệm cận ngang của đồ thị hàm số khi x → + ∞ .
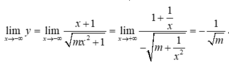
Suy ra đường thẳng y = - 1 m là tiệm cận ngang của đồ thị hàm số.
Vậy m>0 thỏa mãn yêu cầu đề bài.
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
CM
18 tháng 7 2017
Đáp án C
Dễ thấy với m < 0 thì hàm không có tiệm
cận ngang vì x không tiến đến ∞
Với m = 0, hàm có dạng y = x + 1 và cũng
không có tiệm cận ngang
Với m > 0, ta có:
Xét lim x → + ∞ x + 1 m x 2 + 1 = lim x → + ∞ 1 + 1 x m + 1 x = 1 m
Lại có lim x → - ∞ x + 1 m x 2 + 1 = lim x → - ∞ 1 + 1 x - m + 1 x = 1 - m
⇒ Hàm có 2 tiệm cận ngang
CM
18 tháng 3 2018
Ta có
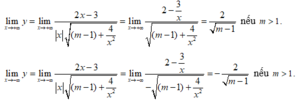
Vậy với m > 1 thì đồ thị hàm số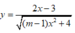 
có hai tiệm cận ngang là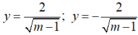 
Chọn đáp án C.
CM
13 tháng 3 2018
Đáp án A.
Ta có 2 x + 3 m x 2 + 1 = 2 x + 3 x 1 m + 1 x 2 ⇒ lim x → − ∞ 2 x + 3 x = lim x → − ∞ 2 x + 3 − x = − 2 và
lim x → + ∞ 2 x + 3 x = lim x → + ∞ 2 x + 3 x = 2 . Từ đó, suy ra các giới hạn lim x → − ∞ 2 x + 3 m x 2 + 1 ; lim x → + ∞ 2 x + 3 m x 2 + 1 tồn tại và hữu hạn khi và chỉ khi các giới hạn lim x → − ∞ m + 1 x 2 ; lim x → + ∞ m + 1 x 2 tồn tại, hữu hạn và khác không. Do lim x → ± ∞ 1 x 2 = 0 các giới hạn vừa nêu tồn tại, hữu hạn và khác 0 khi và chỉ khi m > 0.
Chú ý và Lỗi sai
* Định nghĩa: Cho hàm số y = f x xác định trên a ; + ∞ ; − ∞ ; b ; − ∞ ; + ∞
Nếu lim x → + ∞ f x = y 0 lim x → − ∞ f x = y 0 thì y = y 0 là tiệm cận ngang.
Từ định nghĩa tiệm cận ngang của đồ thị hàm số suy ra các giá trị m cần tìm là các giá trị sao cho tồn tại giới hạn của hàm số đã cho khi x tiến ra + ∞ và khi x tiến ra - ∞ , đồng thời hai giới hạn đó phải khác nhau.
Chọn A.
Phương pháp: Sử dụng điều kiện tiếp xúc của hai đường cong: Hai đường cong f(x) và g(x) tiếp xúc với nhau khi và chỉ khi hệ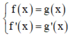
có nghiệm và nghiệm là hoành độ tiếp điểm.
Khi đó tiệm cận ngang của đồ thị hàm số đã cho là: y = m.