Tìm số giá trị nguyên của tham số thực m để hàm số y = x 2 + m x + 6 3 + 2 xác định trên ℝ
A. 9
B. 5
C. 10
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hàm số xác định trên ℝ khi và chỉ khi
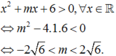
Suy ra các giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán là - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 . Vậy số 9 có giá trị nguyên tham số m .
Phân tích phương án nhiễu.
Phương án B: Sai do HS tính sai biệt thức ∆ = m 2 - 6 < 0 ⇔ - 6 < m < 6 nên tìm được 5 giá trị .
Phương án C: Sai do HS đếm sai. Cụ thể là có 5 số nguyên thuộc [ 0 ; 2 6 ) , khoảng - 2 6 ; 2 6 là khoảng đối xứng nên trong khoảng - 2 6 ; 2 6 có 10 số nguyên.
Phương án D: Sai do HS giải sai như phương án B nhưng đếm sai như phương án C.

Đáp án D.
Hàm số xác định với mọi x ∈ ℝ ⇔ x 2 - 2 m x + 4 > 0 , ∀ x ∈ ℝ ⇒ ∆ ' = m 2 - 4 < 0 ⇔ - 2 < m < 2 .

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
cho em hỏi là tại sao m≠0 mà đkxđ của m lại là -3<m<3 ạ ?
Đáp án A