Gọi (S) là tập hợp đi qua 4 điểm A(2;0;0), B(1;3;0), C(-1;0;3), D(1;2;3). Tính bán kính R của mặt cầu (S) ...
Đọc tiếp
Gọi (S) là tập hợp đi qua 4 điểm A(2;0;0), B(1;3;0), C(-1;0;3), D(1;2;3). Tính bán kính R của mặt cầu (S)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 8 2017
Phương trình tiếp tuyến tại điểm 
là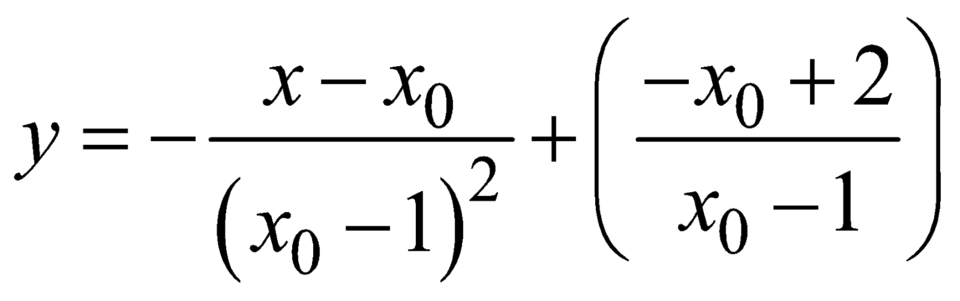 
Tiếp tuyến đi qua điểm A suy ra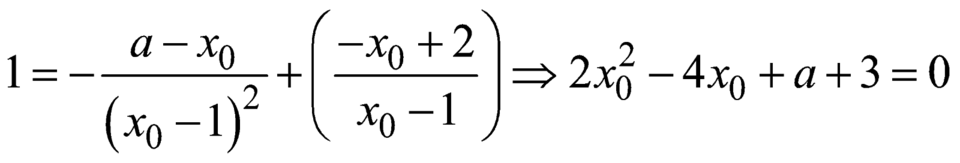 
có duy nhất nghiệm khi a=1. Số phần tử của S là 1.
Đáp án B
CM
10 tháng 4 2019
Đáp án D
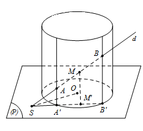
Gọi P là mặt phẳng đi qua S và vuông góc với trục của mặt T . Mặt phẳng P cắt T theo giao tuyến một đường tròn. Chiếu A, B, M theo phương vuông góc với mặt phẳng P ta được các điểm theo thứ tự là A ' , B ' , M ' thẳng hàng với S, trong đó A’,B’ nằm trên đường tròn tâm O trong mặt phẳng P và M’là trung điểm của A’B’. Do đó M’ luôn nằm trên đường tròn đường kính SO trong mặt phẳng P và MM’ vuông góc với P . Vậy MM’ nằm trên mặt trụ T ' chứa đường tròn đường kính SO và có trục song song với trục của mặt trụ T .
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2021
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi phương trình đường thẳng d qua A có dạng: \(y=k\left(x-a\right)+1\)
d tiếp xúc (C) khi và chỉ khi hệ sau có nghiệm:
\(\left\{{}\begin{matrix}\dfrac{-x+2}{x-1}=k\left(x-a\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{-x+2}{x-1}=\dfrac{-\left(x-a\right)}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=x-a-\left(x-1\right)^2\)
\(\Leftrightarrow2x^2-6x+3=-a\) (1)
Để có đúng 1 tiếp tuyến qua A khi (1) có đúng 1 nghiệm
\(\Rightarrow y=-a\) tiếp xúc \(y=2x^2-6x+3\)
\(\Leftrightarrow-a=-\dfrac{3}{2}\Rightarrow a=\dfrac{3}{2}\)
CM
30 tháng 8 2019
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là: y= k( x-a) +1
+ Phương trình hoành độ giao điểm của d và (C) :
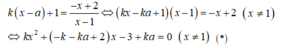
+ Với k= 0, ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
Với k≠0 , d và (C) tiếp xúc nhau khi và chỉ khi (1) có nghiệm kép
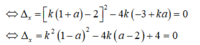
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1) vẽ được đúng tiếp tuyến thì phương trình có đúng một nghiệm k≠ 0.
*Xét 1-a= 0 hay a=1, ta có 4k+ k= 0 hạy k= -1 thỏa.
*Có f(0) = 4≠0 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là .
*Còn lại là trường hợp ∆x= 0 có nghiệm kép khi
Vậy có 2 giá trị của a thỏa mãn đầu bài là a= 1 hoặc a= 3/2.
Chọn A.
CM
18 tháng 4 2017
Chọn đáp án D
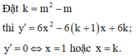
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
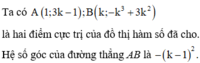
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi
CM
25 tháng 6 2018
Chọn đáp án A.
Suy ra số tập hợp con khác rỗng của S là 2 3 - 1 = 7
Chọn: B