Điều nào sau đây là SAI khi nói về năng lượng trong dao động điều hoà của con lắc lò xo:
A. Động năng và thế năng biến thiên tuần hoàn theo thời gian với chu kỳ bằng một nửa của chu kỳ dao động.
B. Động năng cực đại bằng thế năng cực đại và bằng với cơ năng.
C. Động năng và thế năng biến thiên theo thời gian với tần số bằng tần số dao động.
D. Cơ năng tỉ lệ với bình phương biên độ dao động và độ cứng của lò xo.

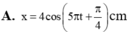
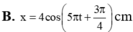
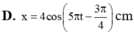

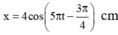
Đáp án C