Cho đoạn thẳng AB = 6cm. Hai đường tròn (A; 4cm) và (B; 3cm) cắt nhau tại C và D. đường tròn tâm A cắt AB tại M, đường tròn tâm B cắt AB tại N
a) Tính AC, AD, BC, BD
b) Chứng minh N là trung điểm của AB
c) Tính MB, MN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

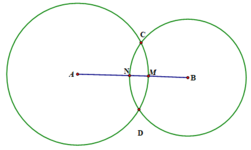


\(a)\)Ta có:
\(M\in\left(A,3\right)\rightarrow AM=3\rightarrow BM=AB-AM=3\)
\(N\in\left(B,4\right)\rightarrow BN=4\rightarrow AN=AB-BN=2\)
\(b)\)Ta có:
\(AM=MB=\frac{1}{2}AB\left(=3\right)\)
\(\rightarrow M\)là trung điểm \(AB\)
B A M N
a)AN=6-4=2(cm)
BM=6-3=3(cm)
b)M là trung điểm của đoạn thẳng AB vì AM =BM(3cm)và M thuộc AB
Đúng thì cho mik nha, thank!

a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: góc OHM=góc ONM=90 độ
=>OHNM nội tiếp
=>góc MON=góc MHN

4.1:
a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=8^2+6^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(CH\cdot CB=CA^2\)
=>\(CH\cdot10=6^2=36\)
=>CH=36/10=3,6(cm)
4.2:
Ta có: ΔCAD cân tại C
mà CB là đường cao
nên CB là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔCAB=ΔCDB
=>\(\widehat{CAB}=\widehat{CDB}\)
mà \(\widehat{CAB}=90^0\)
nên \(\widehat{CDB}=90^0\)
=>BD là tiếp tuyến của (C)
4.3:
Xét (C) có
PA,PM là các tiếp tuyến
Do đó: PA=PM
Xét (C) có
QM,QD là các tiếp tuyến
Do đó: QM=QD
Chu vi tam giác BPQ là:
\(C_{BPQ}=BP+PQ+BQ\)
=BP+PM+BQ+QM
=BP+PA+BQ+QD
=BA+BD
=2BA
=2*8=16(cm)