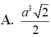
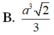
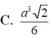
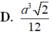
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Ta có: SA = SB = SC =a
⇒ ∆ S B D đ ề u
Gọi O là tâm hình thoi ABCD, I là tâm tam giác đều SBD cạnh a.
Vì AS = AB = AD
Dễ dàng tính được
Xét ∆ A I O vuông tại I có:
⇒ V A . S B D = 1 3 . A I . S S B D = a 2 3 12 (đvtt)
Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)
Đáp án C
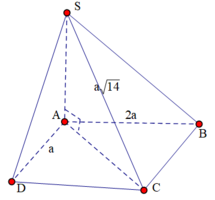
Hai mặt (SAB) và (SAD) đáy S A ⊥ ( A B C D )
S A = S C 2 - A C 2 = S C 2 - A B 2 - A D 2 = 14 a 2 - 4 a 2 - a 2 = 3 a
Ta có
⇒ V S . A B C D = 1 3 S A . d t A B C D = 1 3 S A . A B . A D = 1 3 3 a . 2 a . a = 2 a 3
Đáp án C