Question

[Hoàng Đức Long]

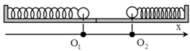
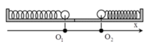
Một lò xo nhẹ có chiều dài tự nhiên l₀, độ cứng k 0   =   16   N / m , được cắt thành hai lò xo có chiều dài lần lượt là l 1   =   0 , 8   l 0   v à   l 2   =   0 , 2 l 0 . Mỗi lò xo sau khi cắt được gắn với vật có cùng khối lượng 0,5 kg. Cho hai con lắc lò xo mắc vào hai mặt tường đối diện nhau và cùng đặt trên mặt phẳng nhẵn nằm ngang (các lò xo đồng trục). Khi hai lò xo chưa biến dạng thì khoảng cách hai vật là 12cm. Lúc đầu, giữ các vật để cho các lò xo đều bị nén đồng thời thả nhẹ để hai vật dao động cùng thế năng cực đại là 0,1 J. Lấy π 2   =   10 . Kể từ lúc thả vật, sau khoảng thời gian ngắn nhất là Δt thì khoảng cách giữa hai vật nhỏ nhất là d. Giá trị  Δt  và d lần lượt là

A. 1 10 s ; 7 , 5 c m                                                    

B.  1 3 s ; 4 , 5 c m               

 C.  1 3 s ; 7 , 5 c m                

D.  1 10 s ; 4 , 5 c m

Answer 1

[Vũ Thành Nam]

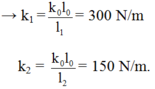
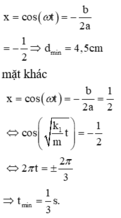
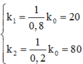
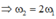
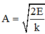
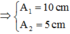
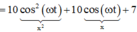
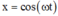
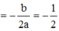
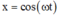
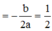
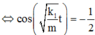
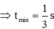
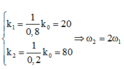
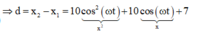
Chọn B

+Độ cứng của các lò xo sau khi cắt:   k 1 = 1 0 , 8 k 0 = 20 k 2 = 1 0 , 2 k 0 = 80 ⇒ ω 2 = 2 ω 1

+Biên độ dao động của các vật:   A = 2 E k ⇒ A 1 = 10 c m A 2 = 5 c m

+Với hệ trục tọa độ như hình vẽ (gốc tạo độ tại vị trí cân bằng của vật thứ nhất), phương trình dao động của các vật là

x 1 = 10 cos ( ω t + π ) x 2 = 12 + 5 cos ( 2 ω t ) ⇒ d = x 2 − x 1 = 10 cos 2 ω t ⏟ x 2 + 10 cos ω t + 7 ⏟ x

d nhỏ nhất khi

x = cos ( ω t ) = − b 2 a = − 1 2 ⇒ d min = 4 , 5 c m

Mặt khác:

x = cos ( ω t ) = − b 2 a = 1 2 ⇔ cos k 1 m t = − 1 2 ⇔ 2 π t = ± 2 π 3 + 2 k π ⇒ t min = 1 3 s

⇒ Chọn B