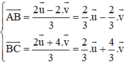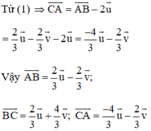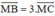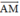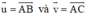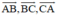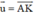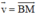Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
Do BN là trung tuyến
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\\\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\\2\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{BC}\end{matrix}\right.\)
Cộng vế với vế:
\(\overrightarrow{AM}+2\overrightarrow{BN}=\dfrac{3}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AM}+\dfrac{4}{3}\overrightarrow{BN}\)
CM
17 tháng 11 2017
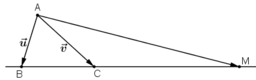
Ta có: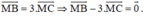 
Theo quy tắc ba điểm ta có:
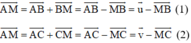
Lấy (1) trừ 3 lần (2) ta được:
CM
13 tháng 1 2018
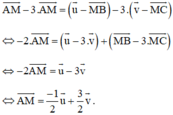
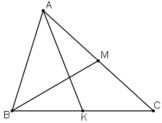
+ K là trung điểm của BC nên ta có:
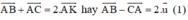
+ M là trung điểm AC nên ta có:
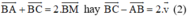
+ Lại có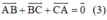 
Cộng (1) với (3) ta được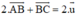 
,
kết hợp với (2) ta được hệ phương trình: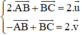 
Giải hệ phương trình ta được
