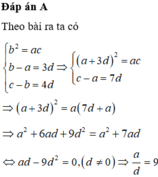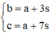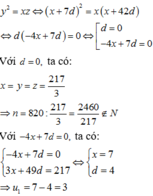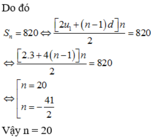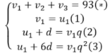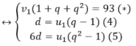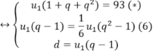Cho ba số a,b,c,d theo thứ tự tạo thành cấp số nhân với công bội khác 1. Biết tổng ba số hạng đầu bằng 148 9 , đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức T=a-b+c-d?
A. T= 101 27 x
B. T= 100 27 .
C. T=- 100 27
D. T= - 101 27