Chọn ngẫu nhiên hai số a và b từ tập A= 2 , 2 2 , 2 3 , . . . , 2 25 . Xác suất để l o g a b là một số nguyên bằng
A. 31 75
B. 31 300
C. 7 50
D. 31 150
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
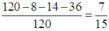

"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?

a: n(omega)=4
n(A)=4
=>P=4/4=1
b: n(omega)=4
n(A)=1; A={5}
=>P(A)=1/4

a. Không gian mẫu: \(C_{10}^3\)
Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)
Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:
- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn
- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn
Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn
Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)
b.
Có 2 số chia hết cho 4 là 4 và 8
Rút ra k thẻ: \(C_{10}^k\) cách
Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)
Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)
\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)
\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)
\(\Rightarrow6< k< 13\)