Cho cấp số nhân ( u n ) thoả mãn u 2 ≥ 100 u 1 ≥ 1 . Đặt f ( x ) = x 3 - 3 x 2 . Biết f ( l o g u 2 ) + 4 = f ( l o g u 1 ) . Tìm số tự nhiên n nhỏ nhất sao cho u n > 10 2018 .
A. 1010.
B. 2020.
C. 2019.
D. 1011.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

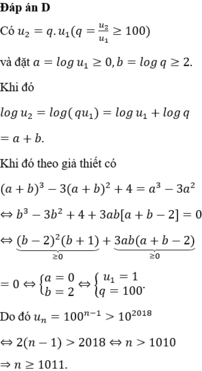



1 ) ( x^2 + 1 )( x^2 + 5 ) = 0
=> x^2 + 1 = 0 hoặc x^2 + 5 = 0
=> x^2 = -1 hoặc x^2 = -5 ( loại vì x^2 >= 0 )
2) =>20x^2 - 4x + 20x - 20x^2 = 16
=> 16x = 16
=> x = 1
3) ( 100 -a )( 100- b ) = 10000 - 100b - 100a - ab
= 100 ( 100 -a - b ) - ab
=> x = -1
sai
đọc kĩ đề bài 1 đi
số giá trị của x!
vậy9 kết quả phải là 0 vì x ko có kết quả nào thõa mản dk trên
