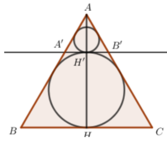
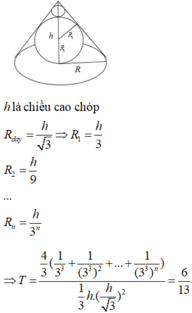
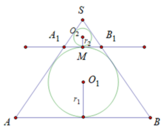
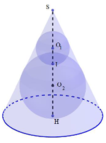
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 1 ;..; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , . . . . . , V n - 1 , V n , lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , . . . . . , S n - 1 , S n , và V là thể tích của khối nón. Tính giá trị của biểu thức T = l i m V 1 + V 2 + . . . + V n V .
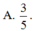
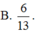
![]()
![]()

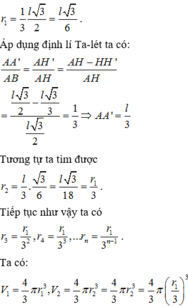

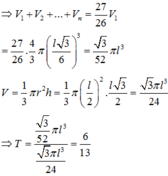


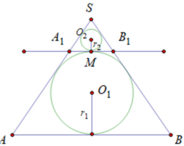
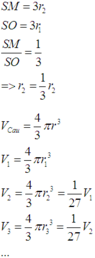
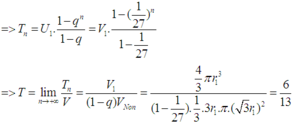
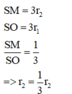
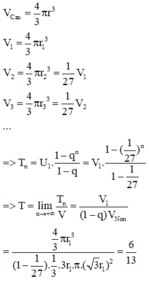

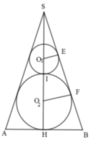
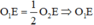 là đường trung bình của tam giác SO
là đường trung bình của tam giác SO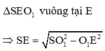
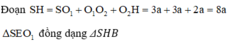
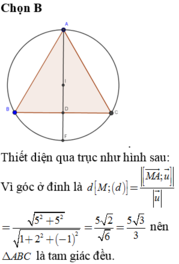
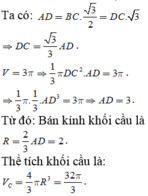
Đáp án đúng : B