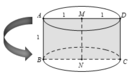
Cho hình chữ nhật ABCD có AB=1 và AD=2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh đường thẳng MN, ta được một hình trụ. Tính thể tích của khối trụ
A. 2 π 3
B. π 3
C. π
D. 10 π 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Công thức tính thể tích khối trụ là V = π r 2 h .Trong đó h là chiều cao của hình trụ, r là bán kính đáy.
Cách giải: Ta có: chiều cao h của khối trụ là AD hoặc BC nên h = 2
Bán kính đáy là r = A B 2 = 1 2
Khi đó ta có thể tích khối trụ cần tìm là V = π r 2 h = π . 1 4 .2 = π 2

Chọn C
Ta có:
![]()
![]()
Hình trụ đã cho có chiều cao là h = MN = AB = 1
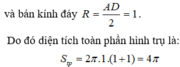

Đáp án B
Hình trụ có bán kính đáy là R = 2 : 2 = 1 ; ; chiều cao là h = 1
Diện tích toàn phần của hình trụ là S t p = 2 π R 2 + 2 π R h = 2 π .1 2 + 2 π .1.1 = 4 π

Đáp án A
Khi quay quanh MN ta được hình trụ có chiều cao h = AB = 1 và bán kính đáy R = A D 2 = 1
Diện tích toàn phần của hình trụ đó là S t p = 2 π R 2 + 2 π R h = 4 π
Đáp án C
Khối trụ tạo thành có bán kính đáy R = A D 2 = 1 ; và chiều cao h = A B = 1. Vậy thể tích khối trụ cần tính là V = π R 2 h = π .1 2 .1 = π .