Trong không gian Oxyz, cho đường thẳng d : x + 2 4 = y - 1 - 4 = z + 2 3 và mặt phẳng (P): 2x-y+2z+1=0. Đường thẳng ∆ đi qua E(-2;1;-2) song song với (P) đồng thời tạo với d góc bé nhất. Biết rằng ∆ có một vector chỉ phương u → = ( m ; n ; 1 ) . Tính T = m 2 - n 2
A. T = -5
B. T = 4
C. T = 3
D. T = -4



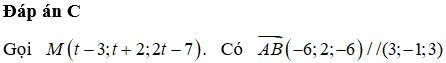
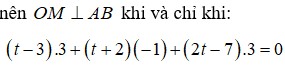
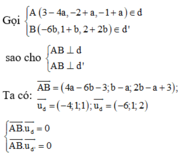


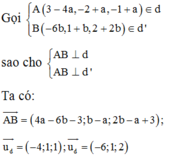

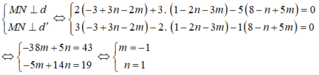

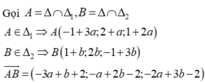
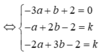
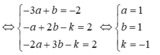

Đáp án D
Phương pháp:
+) Sử dụng công thức
+) Để góc giữa ∆ và d là nhỏ nhất thì
Cách giải :
Do ∆ //(P)
Ta có
Để góc giữa ∆ và d là nhỏ nhất thì
Có g'(x)
= ( 32 m + 40 ) ( 5 m 2 + 8 m + 5 ) - ( 16 m 2 + 40 m + 25 ) ( 10 m + 8 ) 5 m 2 + 8 m + 5 2
Lập BBT ta thấy