Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 2 ; 2 ; 1 , B − 8 3 ; 4 3 ; 8 3 . Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt phẳng (OAB) có phương trình là
A. x + 1 1 = y − 3 − 2 = z + 1 2 .
B. x + 1 1 = y − 8 − 2 = z − 4 2 .
C. x + 1 3 1 = y − 5 3 − 2 = z − 11 6 2 .
D. x + 2 9 1 = y − 2 9 − 2 = z + 5 9 2 .


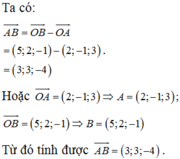
Đáp án A.
Ta có O E E ∈ A B Vecto chỉ phương
của đường thẳng (d) là u → = 1 ; − 2 ; 2 .
Kẻ phân giác O E E ∈ A B suy ra
O A O B = A E B E = 3 4 ⇒ A E → = 3 4 E B → ⇒ E 0 ; 12 7 ; 12 7 .
Gọi I là tâm đường tròn nội tiếp
Δ O A B ⇒ I ∈ O E ⇒ O I → = k O E , → với k > 0.
Tam giác OAB vuông tại O, có bán kính
đường tròn nội tiếp r = 1 ⇒ I O = 2 .
Mà
A E = 15 7 ; O A = 3 ; c os O A B ^ = 3 5 → O E = 12 2 7 s u y r a O E ¯ = 12 7 O I ¯ ⇒ I 0 ; 1 ; 1 .
Vậy phương trình đường thẳng cần tìm là
d : x + 1 1 = y − 3 − 2 = z + 1 2