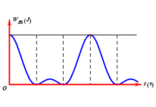
Một con lắc lò xo treo thẳng đứng dao động điều hòa với chu kì T. Đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi của con lắc vào thời gian được cho như hình vẽ. Trong 1 chu kì, khoảng thời gian lò xo bị nén là
A. T 3
B. T 6
C. T 2
D. T 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Từ đồ thị ta thấy rằng khoảng thời giữa hai vị trí thế năng đàn hồi bằng 0 gần nhau nhất chính là khoảng thời gian lò xo bị nén t = T 3 .
Đáp án A

Hướng dẫn:
Lực đàn hồi của vật luôn hướng về vị trí lò xo không biến dạng → lực đàn hồi sẽ đổi chiều khi vật đi qua vị trí lò xo không biến dạng (tại vị trí này thế năng đàn hồi bằng 0) → Từ hình vẽ ta thấy trong khoảng thời gian từ t 1 đến t 2 có 2 vị trí thế năng bằng 0 do vậy sẽ có 2 lần lực đàn hồi đổi chiều.
Đáp án B

Đáp án C
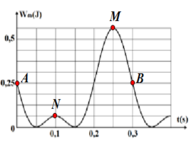
Từ đồ thị ta thấy :
+ Thế năng đàn hồi lớn nhất là 0,5625 J ứng với vị trí lò xo giãn nhiều nhất (biên dưới) – điểm M trên đồ thị
+ Thế năng đàn hồi ở biên trên ứng với vị trí lò xo bị nén cực đại – điểm N trên đồ thị.
Dễ thấy điểm N ứng với thế năng đàn hồi 0,0625 J
Để ý thấy từ điểm A đến điểm B thì đồ thị lặp lại, tức là bằng 1 chu kỳ
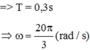
Thay vào (1) tìm được m ≈ 0 , 56 k g

Đáp án C

Mốc tính thế năng đàn hồi được chọn tại vị trí lò xo không biến dạng.
Từ đồ thị ta thấy mỗi ô có thế năng là 0 , 25 4 = 0 , 0625
Thế năng đàn hồi tại vị trí cao nhất: 0 , 0625 = 1 2 k A − Δ l 0 2 ( 1 )
Thế năng đàn hồi cực đại tại vị trí thấp nhất: W d max = 0 , 5625 = 1 2 k A + Δ l 0 2 ( 2 )
Lấy (2) chia (1): 9 = A + Δ l 0 2 A − Δ l 0 2 ⇒ 3 = A + Δ l 0 A − Δ l 0 ⇒ A = 2 Δ l 0 ( 3 )
Từ đồ thị ta thấy chu kì dao động của con lắc là: T = 0 , 3 s
Mặt khác con lắc lò xo treo có chu kì:
T = 2 π m k = 2 π Δ l 0 g ⇒ Δ l 0 = T 2 g 4 π 2 = 0 , 3 2 π 2 4 π 2 = 0 , 0225 m = 2 , 25 c m
⇒ A = 2 Δ l 0 = 4 , 5 c m Thế vào (1): k = 2.0 , 0625 A − Δ l 0 2 = 2.0 , 0625 0 , 045 − 0 , 0225 2 = 247 N / m
⇒ m = T 2 k 4 π 2 = 0 , 3 2 .247 4 π 2 = 0 , 56 k g
Chú ý: Gốc thế năng đàn hồi được chọn tại vị trí lò xo không dãn.