Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 - 6 x 2 + 4 m - 9 x + 4 nghịch biến trên khoảng - ∞ ; - 1 là
A. ( - ∞ ; 0 ]
B. [ - 3 4 ; + ∞ )
C. ( - ∞ ; - 3 4 ]
D. [ 0 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
Hàm số y = f(x) nghịch biến trên D khi và chỉ khi ![]() và bằng 0 tại hữu hạn điểm
và bằng 0 tại hữu hạn điểm
Cách giải:
Ta có: ![]()
Hàm số đã cho nghịch biến trên ![]()
![]()
![]()
![]()
![]()
![]()
Xét hàm số: ![]() ta có:
ta có: ![]()
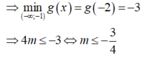
Chọn đáp án D.
Do đó để phương trình f sin x = m có nghiệm trong khoảng (0;p)
thì phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ]
Quan sát đồ thị thấy phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ] khi - 1 ≤ m < 1