Trong không gian, cho hình chữ nhật ABCD có AB=1 và AD=2 Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S t p của hình trụ đó.
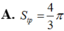
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
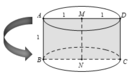
Ta có:
![]()
![]()
Hình trụ đã cho có chiều cao là h = MN = AB = 1
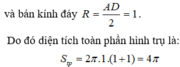

Đáp án B
Hình trụ có bán kính đáy là R = 2 : 2 = 1 ; ; chiều cao là h = 1
Diện tích toàn phần của hình trụ là S t p = 2 π R 2 + 2 π R h = 2 π .1 2 + 2 π .1.1 = 4 π

Đáp án A
Khi quay quanh MN ta được hình trụ có chiều cao h = AB = 1 và bán kính đáy R = A D 2 = 1
Diện tích toàn phần của hình trụ đó là S t p = 2 π R 2 + 2 π R h = 4 π

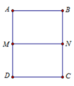
Đáp án B
Hình trụ có bán kính đáy r = A D 2 = 2 2 = 1 , chiều cao h = A B = 1
Diện tích toàn phần hình trụ là S t p = 2 π r l + 2 π r 2 = 2 π .1.1 + 2 π .1 2 = 4 π