Có 5 học sinh không quen biết nhau cùng đến một cửa hàng kem có 6 quầy phục vụ. Xác suất để có 3 học sinh cùng vào 1 quầy và 2 học sinh còn lại vào 1 quầy khác là
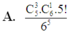
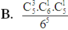
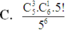
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp giải: Áp dụng các quy tắm đếm cơ bản
Lời giải:
Một người có 6 cách chọn quầy khác nhau => Số phần tử của không gian mẫu là n ( Ω ) = 6 5
Chọn 3 học sinh trong 5 học sinh có C 5 3 cách, chọn 1 quầy trong 6 quầy có C 6 1 cách.
Suy ra có C 5 3 . C 6 1 cách chọn 3 học sinh vào 1 quầy bất kì.
Khi đó, 2 học sinh còn lại sẽ chọn 5 quầy còn lại => có C 5 1 cách.
Do đó, số kết quả thuận lợi cho biến cố là n(X) = C 5 1 . C 5 3 . C 6 1
Vậy P =

Chọn D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố: Có 3 người cùng đến quầy thứ nhất .
Số kết quả thuận lợi của biến cố A là: ![]()
Xác suất của biến cố A: 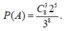

Mỗi người khách có 3 cách chọn quầy nên không gian mẫu là: \(3^8\)
Chọn 3 người khách từ 8 người: \(C_8^3\) cách
Xếp 3 người đó vào quầy 1 có 1 cách, còn lại 5 người khách xếp vào 2 quầy còn lại, mỗi người khách có 2 cách chọn quầy nên 5 người này có \(2^5\) cách chọn quầy
\(\Rightarrow C_8^3.1.2^5\) cách để 3 người đến quầy thứ nhất

Gọi số xe cần tìm là a
Xe đạp cất đi chiếm số phần là: 1 – 1/6 – 5/6
Theo bài ra ta có :
5/6 x a = (1/6 x a - 5) x 10
5/6 x a = 10/6 x a – 50
50 = 5/6 x a
a = 50 x 6 : 5 = 60

Chọn B.
Phương pháp: Sử dụng hoán vị và quy tắc nhân.
Cách giải: Xếp 12 học sinh vào 12 ghế có 12! cách xếp.
Đánh số ghế như sau:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Chọn giới tính nam hoặc nữ có 2 cách.
Xếp nam hoặc nữ ngồi vào các ghế 1, 3, 5, 8, 10,12 có 6!= 720 cách.
Xếp các bạn giới tính còn lại vào 6 ghế còn lại có 6!= 720cách.
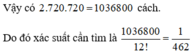

P/s chỉ số sách trong hộp là:
1-1/4=3/4
P/s chỉ số sách trong hộp sau khi bán là
1/2 . 2=2/4
P/s chỉ 50 quyển sách là
3/4-2/4=1/4
Số sách ban đầu là
50:1/4=200(quyển sách )
Đ/s:200 quyển sách
#)Giải :
Người bán hàng mang vào trong hộp là :
1 - 1/4 = 3/4 ( số sách ban đầu )
Sau khi bán 50 quyến sách thì số sách ở quầy = 1/2 hay một nửa số sách trong hộp
=> Số sách lúc đầu mang vào hộp là 3 phần, số sách sau khi bán còn lại trong hộp là 2 phần
=> Số sách người đó đã bán = 1/4 số sách ban đầu trong hộp
Vậy số sách của cửa hàng ban đầu là :
50 : 1/4 = 200 ( quyển sách )
Đ/số : 200 quyển sách.
Đáp án B
Phương pháp giải: Áp dụng các quy tắm đếm cơ bản
Lời giải:
Một người có 6 cách chọn quầy khác nhau => Số phần tử của không gian mẫu là n ( Ω ) = 6 5
Chọn 3 học sinh trong 5 học sinh có C 5 3 cách, chọn 1 quầy trong 6 quầy có C 6 1 cách.
Suy ra có C 5 3 . C 6 1 cách chọn 3 học sinh vào 1 quầy bất kì.
Khi đó, 2 học sinh còn lại sẽ chọn 5 quầy còn lại => có C 5 1 cách.
Do đó, số kết quả thuận lợi cho biến cố là n ( X ) = C 5 1 . C 6 1 . C 5 1
Vậy P = n ( X ) n ( Ω ) = C 5 3 . C 6 1 . C 5 1 6 5