Đội văn nghệ của trường THPT Hùng Vương có 9 học sinh, trong đó có 4 học sinh lớp 12, 3 học sinh lớp 11 và 2 học sinh lớp 10. Hỏi có bao nhiêu cách chọn ra một nhóm có ít nhất 3 học sinh để biểu diễn...

PT

Pham Trong Bach

28 tháng 12 2017

Đội văn nghệ của trường THPT Hùng Vương có 9 học sinh, trong đó có 4 học sinh lớp 12, 3 học sinh lớp 11 và 2 học sinh lớp 10. Hỏi có bao nhiêu cách chọn ra một nhóm có ít nhất 3 học sinh để biểu diễn dịp 26 tháng 3 sao cho mỗi khối có ít nhất một học sinh, biết rằng năng khiếu văn nghệ của các em là như nhau A. 24 B. 315 C. 420 D....

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

28 tháng 12 2017

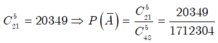
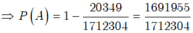
Chọn B

TH1: Nhóm có đúng 3 học sinh có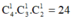 cách chọn

TH2: Nhóm có đúng 4 học sinh có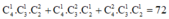 cách chọn

TH3: Nhóm có đúng 5 học sinh có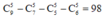 cách chọn

TH4: Nhóm có đúng 6 học sinh có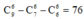 cách chọn

TH5: Nhóm có đúng 7 học sinh có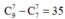 cách chọn

TH6: Nhóm có đúng 8 học sinh có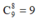 cách chọn

TH7: Nhóm có đúng 9 học sinh có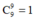 cách chọn

Vậy tổng số có 24 + 72 + 98 + 76 + 35 + 9 + 1 = 315 cách.

Đúng(0)

PT

Pham Trong Bach

21 tháng 3 2018

Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn?

A. 120

B. 102

C. 126

D. 100

#Toán lớp 11

1

CM

Cao Minh Tâm

21 tháng 3 2018

Đúng(0)

PT

Pham Trong Bach

13 tháng 8 2017

Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn?

A. 98

B. 120

C. 150

D. 360

#Mẫu giáo

1

CM

Cao Minh Tâm

13 tháng 8 2017

Đáp án A

Chọn 5 học sinh từ đội văn nghệ của nhà trường, ta xét các trường hợp

TH1. 1 học sinh lớp 12A, 2 học sinh lớp 12B và 2 học sinh lớp 12C → có C 4 1 . C 3 2 . C 2 2 = 12 cách.

TH2. 2 học sinh lớp 12A, 1 học sinh lớp 12B và 2 học sinh lớp 12C → có C 4 2 . C 3 1 . C 2 2 = 18 cách

TH3. 3 học sinh lớp 12A, 1 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 3 . C 3 1 . C 2 1 = 24 cách.

TH4. 1 học sinh lớp 12A, 3 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 1 . C 3 3 . C 2 1 = 8 cách.

TH5. 2 học sinh lớp 12A, 2 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 2 . C 3 2 . C 2 1 = 36 cách.

Đúng(0)

PT

Pham Trong Bach

8 tháng 5 2019

Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn?

A. 120

B. 102

C. 126

D. 100

#Mẫu giáo

1

CM

Cao Minh Tâm

8 tháng 5 2019

Đáp án là C

Đúng(0)

PT

Pham Trong Bach

25 tháng 9 2017

Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn? A. 120 B. 98 C. 150 D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

25 tháng 9 2017

Đúng(0)

PT

Pham Trong Bach

2 tháng 7 2017

Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn? A. 120 B. 98 C. 150 D....

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

2 tháng 7 2017

Đáp án B

Phương pháp.

Chia ra các khả năng có thể có của học sinh các lớp. Tính số cách chọn có thể có của mỗi trường hợp này. Lấy tổng kết quả các khả năng ở trên lại.

Lời giải chi tiết.

Ta xét các trường hợp sau.

Có 1 học sinh lớp 12C có 2 học sinh lớp 12B và 2 học sinh lớp 12A khi đó ta có 2 C 3 2 C 4 2 = 36

cách chọn.

Có 1 học sinh lớp 12C có 3 học sinh lớp 12B và 1 học sinh lớp 12A khi đó ta có 2 C 3 3 C 4 1 = 8 cách chọn.

Có 1 học sinh lớp 12C có 1 học sinh lớp 12B và 3 học sinh lớp 12A khi đó ta có 2 C 3 1 C 4 3 = 24 cách chọn.

Có 2 học sinh lớp 12C có 1 học sinh lớp 12B và 2 học sinh lớp 12A khi đó ta có C 3 1 C 4 2 = 18 cách chọn.

Có 2 học sinh lớp 12C có 2 học sinh lớp 12B và 1 học sinh lớp 12A khi đó ta có C 3 2 C 4 1 = 12 cách chọn.

Vậy tổng số cách chọn là 36 + 8 + 24 + 18 + 12 = 98

Đúng(0)

PT

Pham Trong Bach

10 tháng 7 2019

Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn? A. 98 B. 120 C. 150 D....

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

10 tháng 7 2019

Đáp án A

Chọn 5 học sinh từ đội văn nghệ của nhà trường, ta xét các trường hợp

TH1.1 học sinh lớp 12A, 2 học sinh lớp 12B và 2 học sinh lớp 12C

⇒ có C 4 1 . C 3 2 . C 2 2 = 12 cách

TH2.2 học sinh lớp 12A, 1 học sinh lớp 12B và 2 học sinh lớp 12C

⇒ có C 4 3 . C 3 1 . C 2 2 = 18 cách

TH3.3 học sinh lớp 12A, 1 học sinh lớp 12B và 1 học sinh lớp 12C

⇒ có C 4 3 . C 3 1 . C 2 1 = 24 cách

TH4. 1 học sinh lớp 12A, 3 học sinh lớp 12B và 1 học sinh lớp 12C

⇒ có C 4 1 . C 3 3 . C 2 1 = 8 cách

TH5. 2 học sinh lớp 12A, 2 học sinh lớp 12B và 1 học sinh lớp 12C

⇒ có C 4 2 . C 3 2 . C 2 1 = 36 cách

Đúng(0)

PM

phung minh hieu

4 tháng 4 2015 - olm

Một trường phổ thông có 5 học sinh giỏi lớp 10, 6 học sinh giỏi lớp 11 và 8 học sinh giỏi lớp 12. Cần chọn 4 học sinh để tham gia đội tuyển thi “Đố vui để học”. Hỏi có bao nhiêu cách chọn, nếu mỗi khối có ít nhất một học sinh.

#Toán lớp 9

1

CM

Chibi Moon

5 tháng 4 2015

Vì theo bài mỗi khối có ít nhất 1 hs nên ta có ba phương pháp chọn (không phải là cách chọn):

1. Chọn 1 hs lớp 10: có 5 cách; sau đó chọn 1 hs lớp 11: có 6 cách; cuối cùng chọn 2 hs lớp 12: có 28 cách.

Do đó ở pp này có 5+6+28 = 39 cách.

2. Chọn 1 hs lớp 10: có 5 cách; sau đó chọn 2hs lớp 11: có 15 cách; cuối cùng chọn 1 hs lớp 12: có 8 cách.

Do đó ở pp này có 5+15+8= 28 cách.

3. Chọn 2 hs lớp 10: có 10 cách; sau đó chọn 1 hs lớp 11: có 6 cách; cuối cùng chọn 1 hs lớp 12: có 8 cách.

Do đó ở pp này có 10+6+8=24 cách.

Vậy ta có tổng cộng 39+28+24=91 cách chọn.

Còn nếu chọn 4 người k theo khối lớp thì có tổng cộng 3 876 cách chọn.

Đúng(0)

BC

Big City Boy

1 tháng 5 2023

Tiết mục tốp ca có 9 học sinh đứng thành 1 hàng ngang để biểu diễn văn nghệ, trong đó có 2 học sinh lớp 10, 3 học sinh lớp 11 và 4 học sinh lớp 12. Tính xác suất để 9 học sinh này đứng thành hàng ngang sao cho giữa hai học sinh lớp 10 không có học sinh lớp 11.

#Toán lớp 11

1