Cho tập hợp S có 12 phần tử. Hỏi có bao nhiêu cách chia tập hợp S thành hai tập con (không kể thứ tự) mà hợp của chúng bằng S ?
A . 3 12 + 1 2
B . 3 12 - 1 2
C . 3 12 + 1
D . 3 12 - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có 1 phần tử
A={7}có 1 phần tử
B là tập hợp rỗng
D là tập hợp rỗng
có 1 phần tử
tập hợp A có 4 tập hợp con

bài 1
6 tập hợp con
bài 2
{1};{2};{3};{1;2};{1;3};{2;3}
a){1;2};{1;3};{2;3}
b)có 0
c)có 0
d)6
Bài 1 bạn kia trả lời sai nhé. Có 7 tập hợp con. Tập hợp con thứ 7 chính là tập hợp rỗng. Vì tập rỗng là tập hợp con của mọi tập hợp bạn nhé

1. a) A = { x\(\in\)N | x\(⋮\)5 | x\(\le\)100}
b) B = { x\(\in\)N* | x\(⋮\)11 | x < 100}
c) C = { x\(\in\)N* | x : 3 dư 1 | x < 50}
2. A = { 14; 23; 32; 41; 50}
3. Cách 1: A = { 0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
Cách 2: A = { x\(\in\) N | x < 10}
4. a. A = { 22; 24; 26; 28} có 4 phần tử.
B = { 27; 28; 29; 30; 31; 32} có 6 phần tử.
b. C = { 22; 24; 26}
c. D = { 27; 29; 30; 31; 32}
Chọn A
Cách 1.
Giả sử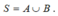 Đặt
Đặt 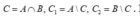 Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là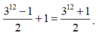
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu S 1 có k phần tử
Vậy số cách chọn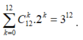
Nhưng trường hợp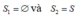 giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách