Có hai hộp đựng bi, mỗi viên bi chỉ mang một màu đen hoặc trắng. Lấy ngẫu nhiên từ mỗi hộp đúng 1 viên bi. Biết tổng số bi trong hai hộp là 20 và xác suất để lấy được hai viên bi đen là
55
84
. Xác suất để lấy được hai viên bi trắng là A.
1
84
B.
1
28
C.
1
14
D.
29
84
...
Đọc tiếp
Có hai hộp đựng bi, mỗi viên bi chỉ mang một màu đen hoặc trắng. Lấy ngẫu nhiên từ mỗi hộp đúng 1 viên bi. Biết tổng số bi trong hai hộp là 20 và xác suất để lấy được hai viên bi đen là 55 84 . Xác suất để lấy được hai viên bi trắng là
A. 1 84
B. 1 28
C. 1 14
D. 29 84
)
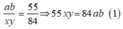
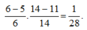
Chọn B
Lời giải.
Giả sử hộp thứ nhất có x viên bi, trong đó có a viên bi đen;
hộp thứ hai có y viên bi, trong đó có b viên bi đen
Điều kiện: x , y , a , b là các số nguyên dương và
Theo giả thiết, ta có
Từ ( 2 ) ⇔ 55 x y = 84 a b
suy ra xy chia hết cho 84
Mặt khác, ta có
nên xy = 84 (3)
Từ (1) và (3), ta được x = 14 y = 6
Từ (3) và (2), suy ra ab = 55 nên a là ước của 55
Lại có 55 6 ≤ 55 b = a ≤ 14 nên a = 11
Với a= 11, ta được b = 5
Vậy xác suất để được 2 bi trắng là