Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Giả sử hộp 1 có viên bi, trong đó có a viên bi đen.
Hộp 2 có y viên bi, trong đó có b viên bi đen.
x, y, a, b là những số nguyên dương, ![]() )
)
Từ giả thiết x + y = 20, 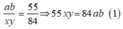
Từ đó ta có xy chia hết cho 84
Mặt khác ![]() suy ra xy = 84 ta được x = 14, y = 6
suy ra xy = 84 ta được x = 14, y = 6
Thay vào (1) ta được ab = 55 nên a là ước của 55. Do a ≤ 14 nên a = 11 suy ra b = 5.
Vậy xác suất để lấy được 2 bi trắng 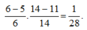

Chọn B
Lời giải.
Giả sử hộp thứ nhất có x viên bi, trong đó có a viên bi đen;
hộp thứ hai có y viên bi, trong đó có b viên bi đen
Điều kiện: x , y , a , b là các số nguyên dương và
![]()
Theo giả thiết, ta có
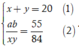
Từ ( 2 ) ⇔ 55 x y = 84 a b
suy ra xy chia hết cho 84
Mặt khác, ta có
![]()
nên xy = 84 (3)
Từ (1) và (3), ta được x = 14 y = 6
Từ (3) và (2), suy ra ab = 55 nên a là ước của 55
Lại có 55 6 ≤ 55 b = a ≤ 14 nên a = 11
Với a= 11, ta được b = 5
Vậy xác suất để được 2 bi trắng là
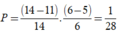

Chọn A
Lời giải
Không gian mẫu là số sách chọn ngẫu nhiên mỗi hộp 1 viên bi
Số phần tử của không gian mẫu là Ω = C 15 1 . C 18 1
Gọi X là biến cố "2 viên bi lấy ra từ mỗi hộp có cùng màu"
Ta có các kết quả thuận lợi cho biến cố X như sau
● Hộp A lấy ra 1 bi trắng và hộp B lấy ra 1 bi trắng, có C 4 1 . C 7 1 cách
● Hộp A lấy ra 1 bi đỏ và hộp B lấy ra 1 bi đỏ, có C 5 1 . C 6 1 cách
● Hộp A lấy ra 1 bi xanh và hộp B lấy ra 1 bi xanh, có C 6 1 . C 5 1 cách
Suy ra số phần tử của biến cố
![]()
Vậy xác suất cần tính
P ( X ) = Ω x Ω = 44 135

Ta có số cách chọn một viên bi trong hộp là 14.13 = 182
A: “Sơn lấy màu xanh, Tùng lấy màu xanh”
Công đoạn 1: Sơn lấy màu xanh có 8 cách
Công đoạn 2: Tùng lấy màu xanh có 7 cách vì Sơn lấy xong không trả lại vào hộp.
Theo quy tắc nhân, tập A có 8.7 = 56 (phần tử)
\( \Rightarrow P\left( A \right) = \frac{{56}}{{182}} = \frac{4}{{13}}\)
B: “Sơn lấy màu đỏ, Tùng lấy màu xanh”
Công đoạn 1: Sơn lấy màu đỏ có 6 cách
Công đoạn 2: Tùng lấy màu xanh có 8 cách
Theo quy tắc nhân, tập B có 6.8 = 48 (phần tử)
\( \Rightarrow P\left( B \right) = \frac{{48}}{{182}} = \frac{{24}}{{91}}\)
C: “Bạn Tùng lấy được viên bi màu xanh” nên \(C = A \cup B\)
\( \Rightarrow P\left( C \right) = P\left( A \right) + P\left( B \right) = \frac{4}{{13}} + \frac{{24}}{{91}} = \frac{4}{7}\)
Vậy xác suất để bạn Tùng lấy được viên bi màu xanh là \(\frac{4}{7}.\)

Không gian mẫu: \(C_{14}^5\)
Các cách chọn thỏa mãn gồm có: (1 đỏ 1 vàng 3 xanh), (2 đỏ 1 vàng 2 xanh), (1 đỏ 2 vàng 2 xanh)
Số cách: \(C_5^1C_6^1C_3^3+C_5^2C_6^1C_3^2+C_5^1C_6^2C_3^2\)
Xác suất: \(P=\dfrac{C_5^1C_6^1C_3^3+C_5^2C_6^1C_3^2+C_5^1C_6^2C_3^2}{C_{14}^5}=...\)
Quảng cáo trắng trợn ghê tar :3 Cơ mà có mod Lâm là đủ rồi á THẦY :)

Không gian mẫu là chọn ngẫu nhiên mỗi hộp 2 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh . Ta liệt kê các trường hợp thuận lợi của không gian biến cố A như sau:
● Trường hợp 1. Chọn hộp thứ nhất 2 viên bi đỏ, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Chọn hộp thứ nhất 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 3. Chọn hộp thứ nhất 2 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi đỏ hoặc 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 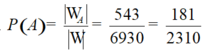
Chọn B.

Gọi A là biến cố "Chọn được 2 viên bi xanh"; B là biến cố "Chọn được 2 viên bi đỏ", C là biến cố "Chọn được 2 viên bi vàng" và X là biến cố "Chọn được 2 viên bi cùng màu".
Ta có X = A ∪ B ∪ C và các biến cố đôi một xung khắc.
Do đó, ta có: P(X)=P(A)+P(B)+P(C) .
Mà: 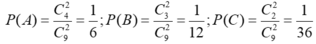
Vậy 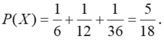
Chọn A.


\(n\left(\Omega\right)=C^2_{13}\cdot C^2_{13}\)
\(n\left(A\right)=C^2_7\cdot C^2_{13}+C^2_6\cdot C^2_{13}+C^2_5\cdot C^2_{13}+C^2_8\cdot C^2_{13}\)
=>P(A)=5772/6084=37/39