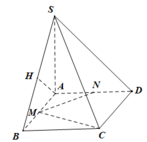
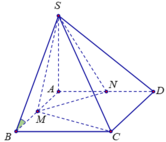
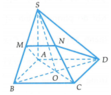
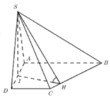
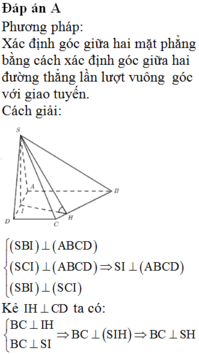
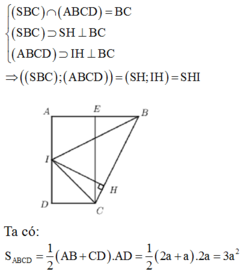
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45 0 . Gọi M, N lần lượt là trung điểm của AB, AD. Tính thể tích khối chóp S.CDMN theo a
A . 5 a 3 8
B . a 3 8
C . 5 a 3 24
D . a 3 3


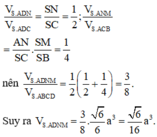

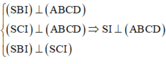
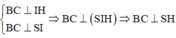
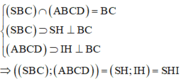
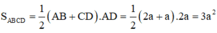
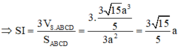
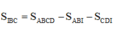
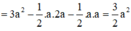
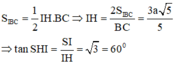


Đáp án C
=> SA = AB = a