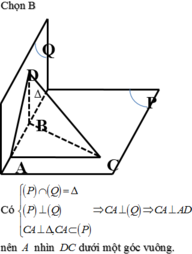
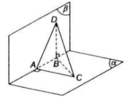
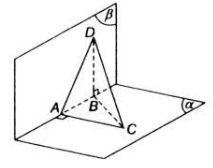
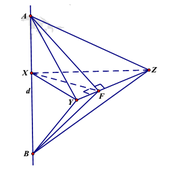
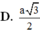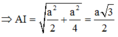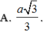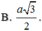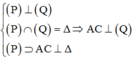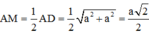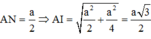Cho mặt phẳng (P) và (Q) vuông góc với nhau theo giao tuyến ∆ . Trên đường thẳng ∆ lấy hai điểm A, B với AB=a. Trong mặt phẳng (P) lấy điểm C và trong mặt phẳng (Q) lấy điểm D sao cho AC, BD cũng vuông góc với ∆ và AC=AB=BD. Bán kính mặt cầu ngoại tiếp tứ diện ABCD là :
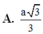
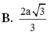
![]()