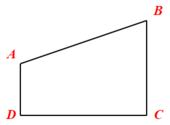
Tứ giác ABCD ( hình bên ) nối ý đúng cho tên các góc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
31 tháng 10 2023
a) Góc đỉnh A, cạnh AB, AD có số đo là 90o
Góc đỉnh D, cạnh DA, DC có số đo là 90o
Góc đỉnh B, cạnh BA, BC có số đo là 120o
Góc đỉnh C, cạnh CB, CD có số đo là 60o
b) AB và AD là cặp cạnh vuông góc với nhau
DA và DC là cặp cạnh vuông góc với nhau
c) AB và DC là cặp cạnh song song với nhau
PT
2
CM
10 tháng 2 2018
Các góc trong hình tứ giác ABCD là:
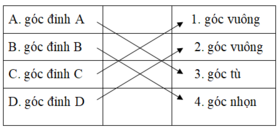
Góc nhọn đỉnh A ; cạnh AB, AD.
Góc tù đỉnh B; cạnh BA, BC.
Góc vuông đỉnh C; cạnh CB, CD.
Góc vuông đỉnh D; cạnh DA, DC.
23 tháng 10 2023
Mặt đáy: (ABCD),(A'B'C'D')
Đỉnh: A,B,C,D,A',B',C',D'
Cạnh bên: AA',BB',CC',DD'
Mặt bên: (AA'D'D), (BB'C'C), (ABB'A')
Cạnh đáy: AB,BC,CD,DA,A'B',B'C',C'D',D'A'
NV
Nguyễn Việt Dũng
CTVVIP
23 tháng 8 2023
a) Các cặp cạnh vuông góc với nhau trong hình trên là: AB và AD ; DA và DC
b) Các cặp cạnh cắt nhau mà không vuông góc với nhau là: AB và BC; BC và CD
16 tháng 4 2021
b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
16 tháng 4 2021
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)