Một thanh kim loại MN dài l = 4,0 cm và khối lượng m = 4,0 g được treo thẳng ngang bằng hai dây kim loại cứng song song cùng độ dài AM và CN trong từ trường đều. Cảm ứng từ của từ trường này có có độ lớn B = 0,10 T, hướng vuông góc với thanh MN và chếch lên phía trên hợp với phương thẳng đứng một góc α . Lúc đầu, hai dây treo AM và CN nằm trong mặt phẳng thẳng đứng. Sau đó, cho dòng điện cường độ I = 10 A chạy qua thanh MN. Lấy g ≈ 10 m/ s 2 . Xác định góc lệch γ của mặt phẳng chứa hai dây treo AM và CN so với mặt phẳng thẳng đứng trong hai trường hợp : góc α = 90 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu cảm ứng từ B - hướng vuông góc với dòng điện I và chếch lên phía trên hợp với phương thẳng đứng góc α, thì theo quy tắc bàn tay trái, lực từ do từ trường tác dụng lên dòng điện I sẽ hướng vuông góc với B - và hợp với phương thẳng đứng góc β = π /2 - α trong cùng mặt phăng vuông góc với dòng điện I như Hình 19-20.3G. Khi đó, hợp lực R - của lực từ F - và trọng lực P - của thanh MN sẽ hợp với phương thẳng đứng một góc γ đúng bằng góc lệch của mặt phẳng chứa hai dây treo AM và CN so với mặt phẳng thẳng đứng của chúng sao cho R - có độ lớn và hướng được xác định theo các công thức :
R 2 = F 2 + P 2 – 2Fpcos β = F 2 + P 2 – 2Fpsin α
Từ đó ta suy ra:
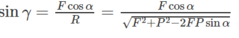
Khi α = 60 °
Vì lực từ F = BIl = 40. 10 - 3 N và trọng lực P = mg ≈ 40. 10 - 3 N, nên F = P.
Thay vào ta có
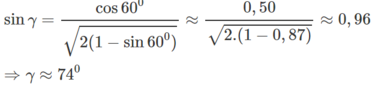

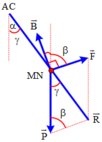
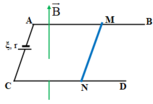
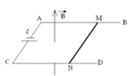
Chọn mặt phẳng hình vẽ, là mặt phẳng thẳng đứng vuông góc với MN, chiều dòng điện hướng từ ngoài vào trong. Cảm ứng từ nằm trong mặt phẳng hình vẽ và chếnh lên trên, theo quy tắc bàn tay trái, hướng của lực từ có dạng như hình vẽ β = 90 0 − α = 30 0 , có độ lớn F = B I = 0 , 04 N .
Trọng lực hướng thẳng đứng từ trên xuống, có độ lớn P = m g = 0 , 04 N = F . Khi cân bằng thì hợp lực R → = F → + P → phải cùng phương ngược chiều với lực căng của hai sợi dây 2 T → ở vị trí như hình vẽ.
Từ tam giác cân có góc ở đỉnh β = 30 0 ⇒ γ = 75 0
Chọn A.

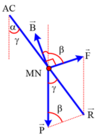
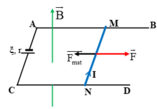
Chọn mặt phẳng hình vẽ, là mặt phẳng thẳng đứng vuông góc với MN, chiều dòng điện hướng từ ngoài vào trong. Cảm ứng từ nằm trong mặt phẳng hình vẽ và chếnh lên trên, theo quy tắc bàn tay trái, hướng của lực từ có dạng như hình vẽ, có độ lớn BIl=0,25
Trọng lực hướng thẳng đứng từ trên xuống, cỏ độ lớn P=mg=4F . Khi cân bằng thì hợp lực R → = F → + P → phải ở vị trí như hình vẽ.
Áp dụng định lý hàm số sin cho tam giác:
F sin γ = P sin β + γ ⇒ 1 sin γ = 4 sin 60 0 + γ ⇒ γ = 13 , 9 o
Chọn D

Đáp án: C
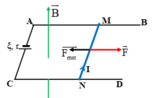
Cường độ dòng điện chạy trong thanh MN là:
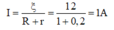
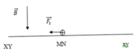
Các lực tác dụng lên thanh MN là
![]()
Xét theo phương chuyển động, ta có:
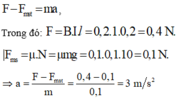

Đáp án C
Ta có: F t = m a
⇒ B I l sin α = m a
⇒ I = m a B l sin α = 0 , 2.2 0 , 2.0 , 2 sin 90 ° = 10 A .

Đáp án C
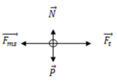
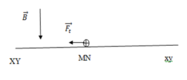
Các lực tác dụng lên thanh MN là P → , F → t , f → m s , N →
Xét theo phương chuyển động F t − F ms = ma , trong đó
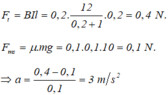

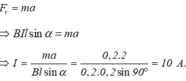
Nếu cảm ứng từ B - hướng vuông góc với dòng điện I và chếch lên phía trên hợp với phương thẳng đứng góc α, thì theo quy tắc bàn tay trái, lực từ do từ trường tác dụng lên dòng điện I sẽ hướng vuông góc với B - và hợp với phương thẳng đứng góc β = π /2 - α trong cùng mặt phăng vuông góc với dòng điện I như Hình 19-20.3G. Khi đó, hợp lực R - của lực từ F - và trọng lực P - của thanh MN sẽ hợp với phương thẳng đứng một góc γ đúng bằng góc lệch của mặt phẳng chứa hai dây treo AM và CN so với mặt phẳng thẳng đứng của chúng sao cho R - có độ lớn và hướng được xác định theo các công thức :
R 2 = F 2 + P 2 – 2Fpcos β = F 2 + P 2 – 2Fpsin α
Từ đó ta suy ra:
Khi α = 90 ° , thì cos90 ° = 0, nên sin γ = 0 và γ = 0