Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng ∆ DNE ∼ ∆ MNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


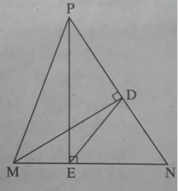
Ta có MD = MN.sinN và MD = DP.tgP nên từ đó suy ra D P = M N . sin N t g P

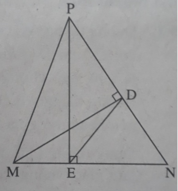
Ta có MD = MPsinP, suy ra
S M N P = 1 2 . N P . M D = 1 2 . M P . N P . sin P

a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
Do đó: MDHE là hình chữ nhật

b: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

Câu hỏi của Ţɦôйǥ ßáø - Toán lớp 8 - Học toán với OnlineMath
Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên D N M N = E N P N Hai tam giác DNE và MNP đồng dạng vì có góc N chung và D N M N = E N P N