Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

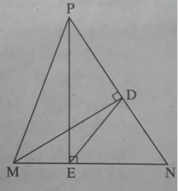
Ta có MD = MN.sinN và MD = DP.tgP nên từ đó suy ra D P = M N . sin N t g P

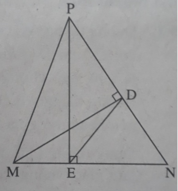
Ta có MD = MPsinP, suy ra
S M N P = 1 2 . N P . M D = 1 2 . M P . N P . sin P

b: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

b: \(\widehat{NMH}+\widehat{N}=90^0\)
\(\widehat{P}+\widehat{N}=90^0\)
Do đó: \(\widehat{NMH}=\widehat{P}\)

Áp dụng hệ thức lượng trong tam giác vuông có:
\(MD^2=ND.DP\)\(\Rightarrow ND=\dfrac{MD^2}{DP}=\dfrac{12^2}{16}=9cm\)
\(\dfrac{1}{DK^2}=\dfrac{1}{ND^2}+\dfrac{1}{DM^2}=\dfrac{25}{1296}\)
\(\Rightarrow DK=\dfrac{36}{5}\) (cm)
Vậy...

Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên D N M N = E N P N Hai tam giác DNE và MNP đồng dạng vì có góc N chung và D N M N = E N P N