Cho hình chóp ABCD có đáy BCD là tam giác vuông cân tại B, CD= a 2 , AB vuông góc với mặt phẳng đáy, AB=b. Khoảng cách từ B đến (ACD) là
A. a b 2 b 2 + a 2
B. 2 b 2 + a 2 a b
C. 1 a b
D. a b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
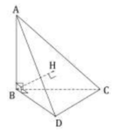
Em nhận thấy, AB, BC, BD đôi một vuông góc nên em có:
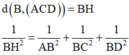
(Với H là hình chiếu vuông góc của B trên (ACD))
Em có tam giác BCD vuông cân tại B, CD = a 2 nên BC = BD = a
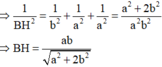
Công thức giải nhanh: Nếu hình chóp O.ABC có OA, OB và OC đôi một vuông góc với nhau thì
d O , ABC = OH và 1 OH 2 = 1 OA 2 + 1 OB 2 + 1 OC 2

Chọn đáp án D
+ Gọi H là trung điểm SB. Do tam giác SAB vuông tại A, SBC vuông tại C suy ta HA = HB = HS = HC
Suy ra H là tâm mặt cầu.
+ Gọi I là hình chiếu của H lên (ABC). Do HA = HB = HC , suy ra IA = IB = IC
Suy ra I là trung điểm AC. Gọi P là trung điểm BC, do tam giác ABC vuông cân, suy ra
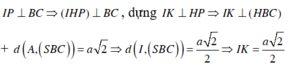
Áp dụng hệ thức
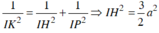
\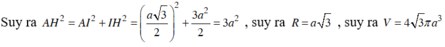

1.
Gọi O là giao điểm AC và BD, Q là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\\OQ\perp AB\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SOQ\right)\)
Từ O kẻ \(OH\perp SQ\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(OQ=\dfrac{BC}{2}=\dfrac{AB}{2}=\dfrac{a}{2}\) ; \(SO=\sqrt{SA^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\)
\(\dfrac{1}{OH^2}=\dfrac{1}{OQ^2}+\dfrac{1}{SO^2}=\dfrac{14}{3a^2}\Rightarrow OH=a\sqrt{\dfrac{14}{3}}\)
\(d\left(P;\left(SAB\right)\right)=2d\left(O;\left(SAB\right)\right)=2OH=2a\sqrt{\dfrac{14}{3}}\)
2.
Câu này đề đúng ko nhỉ? Vì thấy quá nhiều dữ kiện thừa thãi.
Từ \(\overrightarrow{IA}=-2\overrightarrow{IH}\Rightarrow I;A;H\) thẳng hàng
Mà ABC vuông cân tại A \(\Rightarrow AI\perp BC\Rightarrow AH\perp BC\)
Từ K kẻ \(KP||BC\) (P thuộc AH) \(\Rightarrow KP\perp AH\)
\(\left\{{}\begin{matrix}KP\in\left(SAB\right)\Rightarrow SH\perp KP\\KP\perp AH\end{matrix}\right.\) \(\Rightarrow KP\perp\left(SAH\right)\)
\(\Rightarrow KP=d\left(K;\left(SAH\right)\right)\)
\(KP=\dfrac{1}{2}IB\) (đường trung bình); \(IB=\dfrac{1}{2}BC=\dfrac{1}{2}AB\sqrt{2}=a\Rightarrow KP=\dfrac{a}{2}\)

Xét mặt phẳng đáy (ABCD) là hình thang cân. Kéo dài AC cắt BD tại I ta thu được tam giác đều ICD.
Do đó AD và BC đồng thời là đường cao và là đường trung tuyến của tam giác ICD. Suy ra O là trọng tâm của tam giác ICD (Với O là giao của AD và BC)
Ta có: \(AD=\sqrt{CD^2-AC^2}=a\sqrt{3}\)
\(\Rightarrow OA=\dfrac{1}{3}a\sqrt{3}\)
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và có giao tuyến là SO. Do đó SO vuông góc với (ABCD)
Xét tam giác SOB vuông tại O ta có:
\(SO=\sqrt{SA^2-OA^2}=\dfrac{\sqrt{15}}{3}a\)
Vậy khoảng cách từ S đến mặt phẳng (ABCD) là \(\dfrac{\sqrt{15}}{3}a\)
Ta có: \(S_{ABCD}=\dfrac{3}{4}.S_{ICD}=\dfrac{3}{4}.\dfrac{AD.CI}{2}=\dfrac{3}{8}.a\sqrt{3}.2a=\dfrac{3\sqrt{3}}{4}a^2\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{15}}{3}a.\dfrac{3\sqrt{3}}{4}a^2=\dfrac{\sqrt{5}}{4}a^3\)

Xét mặt phẳng đáy (ABCD) là hình thang cân. Kéo dài AC cắt BD tại I ta thu được tam giác đều ICD.
Do đó AD và BC đồng thời là đường cao và là đường trung tuyến của tam giác ICD. Suy ra O là trọng tâm của tam giác ICD (Với O là giao của AD và BC)
Ta có: \(AD=\sqrt{CD^2-AC^2}=a\sqrt{3}\)
\(\Rightarrow OA=\dfrac{1}{3}a\sqrt{3}\)
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và có giao tuyến là SO. Do đó SO vuông góc với (ABCD)
Xét tam giác SOB vuông tại O ta có:
\(SO=\sqrt{SA^2-OA^2}=\dfrac{\sqrt{15}}{3}a\)
Vậy khoảng cách từ S đến mặt phẳng (ABCD) là \(\dfrac{\sqrt{15}}{3}a\)
Ta có: \(S_{ABCD}=\dfrac{3}{4}.S_{ICD}=\dfrac{3}{4}.\dfrac{AD.CI}{2}=\dfrac{3}{8}.a\sqrt{3}.2a=\dfrac{3\sqrt{3}}{4}a^2\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{15}}{3}a.\dfrac{3\sqrt{3}}{4}a^2=\dfrac{\sqrt{5}}{4}a^3\)

Đáp án A.
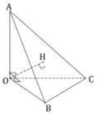
Theo giả thiết ta có SO ⊥ (ABC). Gọi D là điểm đối xưng với B qua O
=> ABCD là hình vuông => AB//CD
=> d(AB;SC) = d(AB;(SCD)) = d(E;(SCD)) = 2d(O;(SCD))(Với E, F lần lượt là trung điểm của AB và CD).
Áp dung tính chất tứ diện vuông cho tứ diện OSCD ta có:
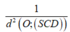
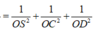
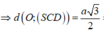
![]()
Đáp án A
Công thức giải nhanh: Nếu hình chóp O.ABC có OA, OB và OC đôi một vuông góc với nhau thì