K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
6 tháng 2 2019
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0; 2019) để l i m   9 n + 3 n + 1 5 n + ...
Đọc tiếp

Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0; 2019) để l i m   9 n + 3 n + 1 5 n + 9 n + a ≤ 1   2187 ?

A. 2011

B. 2018

C. 2019

D. 2012
#Toán lớp 11
1
CM
Cao Minh Tâm
6 tháng 2 2019

Đúng(0)
PT
Pham Trong Bach
9 tháng 3 2019
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2019) để l i m 9 n + 3 n + 1 5 n + ...
Đọc tiếp

Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2019) để l i m 9 n + 3 n + 1 5 n + 9 n + a ≤ 1 2187 ?

A. 2018.      

B. 2011.      

C. 2012.      

D. 2019.
#Mẫu giáo
1
CM
Cao Minh Tâm
9 tháng 3 2019

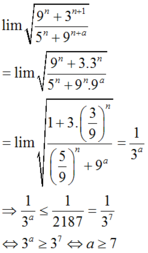
Kết hợp điều kiện đề bài

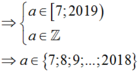
Vậy có 2018 - 7 + 1 = 2012    giá trị của a thỏa mãn.

Chọn C.

Đúng(0)
PT
Pham Trong Bach
5 tháng 5 2018
Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-2017;2017] để hàm số y = x 3 − 6 x 2 + m x + 1  đồng biến trên khoảng 0 ; + ∞ A. 2030 B. 2005 C. 2018 D. 2006...
Đọc tiếp

Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-2017;2017] để hàm số y = x 3 − 6 x 2 + m x + 1  đồng biến trên khoảng 0 ; + ∞

A. 2030

B. 2005

C. 2018

D. 2006
#Mẫu giáo
1
CM
Cao Minh Tâm
5 tháng 5 2018

Đáp án D

giá trị nguyên của tham số m cần tìm

Đúng(0)
PT
Pham Trong Bach
4 tháng 11 2019
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m x 4 - m - 5 x 2 - 3  đồng biến trên khoảng (0;+¥). A. 6    B. 4    C. 3    D. 5 ...
Đọc tiếp

Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m x 4 - m - 5 x 2 - 3  đồng biến trên khoảng (0;+¥).

A. 6   

B. 4   

C. 3   

D. 5 
#Mẫu giáo
1
CM
Cao Minh Tâm
4 tháng 11 2019

Đúng(0)
PT
Pham Trong Bach
19 tháng 4 2019

Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-281;2018] để hàm số  y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng (1;+∞).

A. 2007.

B. 2030.

C. 2005.

D. 2018.
#Mẫu giáo
1
CM
Cao Minh Tâm
19 tháng 4 2019

Đúng(0)
L
Lana(Nana)
4 tháng 2 2023

1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)

2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
#Toán lớp 10
1
HP
Hội Phạm Xuân
25 tháng 11 2023

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.

mình trình bày hơi dài mong bạn thông cảm loading...  

Đúng(0)
TT
Thái Thùy Linh
6 tháng 2 2021

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x4-2x2+3-2m=0 có nghiệm thuộc (-2;2) ?

 

 
#Toán lớp 12
1
NN
Nguyễn Ngọc Lộc
6 tháng 2 2021

- Đặt \(a=x^2\left(a\ge0\right)\)

PTTT \(a^2-2a-2m+3=0\)

Có : \(\Delta^,=\left(-1\right)^2-\left(-2m+3\right)=1+2m-3=2m-2\)

- Theo viet : \(\left\{{}\begin{matrix}a_1+a_2=2\\a_1a_2=3-2m\end{matrix}\right.\)

- Để phương trình đề có nghiệm :

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta^,\ge0\\a_1+a_2>0\\a_1a_2\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2m-2\ge0\\3-2m\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le\dfrac{3}{2}\end{matrix}\right.\)

\(\Rightarrow1\le m\le\dfrac{3}{2}\) ( * )

- Lại có : \(x^4-2x^2=3-2m\)

- Đặt \(f\left(x\right)=x^4-2x^2\)

- Ta có đồ thị của hàm số :

- Theo đồ thị hàm số để phương trình có nghiệm thuộc ( -2; 2 )

\(\Leftrightarrow-1\le3-2m\le8\)

\(\Leftrightarrow-\dfrac{5}{2}\le m\le2\) ( ** )

- Kết hợp điều kiện  ( * ) và ( ** ) ta được : \(m\in\left[1;\dfrac{3}{2}\right]\)

Vậy có 1 giá trị m thỏa mãn điều kiện đề bài ( m = 1 ) .

Đúng(1)
NV
Nguyễn Văn Tư
1 tháng 1 2023

Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=|3x⁴-mx³+6x²+m-3| đồng biến trên khoảng (0- dương vô cùng)
#Toán lớp 12
0
PT
Pham Trong Bach
20 tháng 10 2018
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0  có nghiệm A. 3 B. 7 C. 6 D. 4...
Đọc tiếp

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0  có nghiệm

A. 3

B. 7

C. 6

D. 4
#Mẫu giáo
1
CM
Cao Minh Tâm
20 tháng 10 2018

Đúng(0)
PT
Pham Trong Bach
1 tháng 12 2018
Cho hàm số f ( x ) = m x 4 + 2 x 2 - 1 với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m thuộc khoảng (-2018;2018) sao cho hàm số đã cho đồng...
Đọc tiếp

Cho hàm số f ( x ) = m x 4 + 2 x 2 - 1 với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m thuộc khoảng (-2018;2018) sao cho hàm số đã cho đồng biến trên khoảng (0;1/2)?

A.2022

B.4032

C.4

D.2014
#Toán lớp 12
1
CM
Cao Minh Tâm
1 tháng 12 2018

Chọn D

dIunLzxA2vhM.png.

MEC1eBIygLCM.png: TuYX3tKUeNv0.png Hàm số đồng biến trên iUollBmEuI49.pngLmPu9mQmURcU.png thỏa mãn.

WueRkhJUhVq1.png:

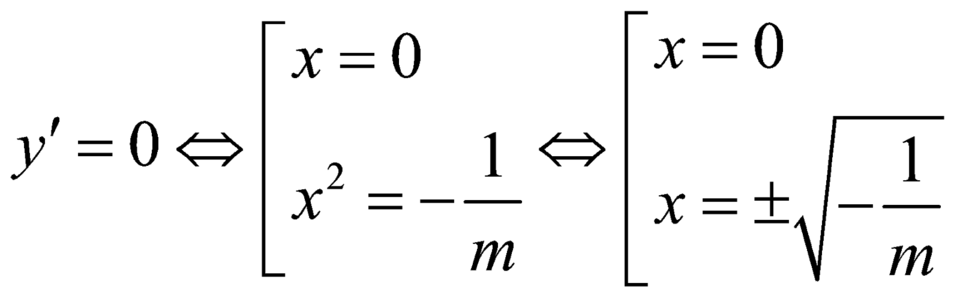sUUq1hweDPqx.png.

BBT :

qbvIqbkhqrp4.png

Dựa vào BBT, hàm số đồng biến trên khoảng

WzT3UKREKPxs.pngWx5gF7n4xrA7.pngul3DURmcnQW1.png.

So với điều kiện XHypIxW1CFhW.png.

 

Mặt khác, theo giả thiết 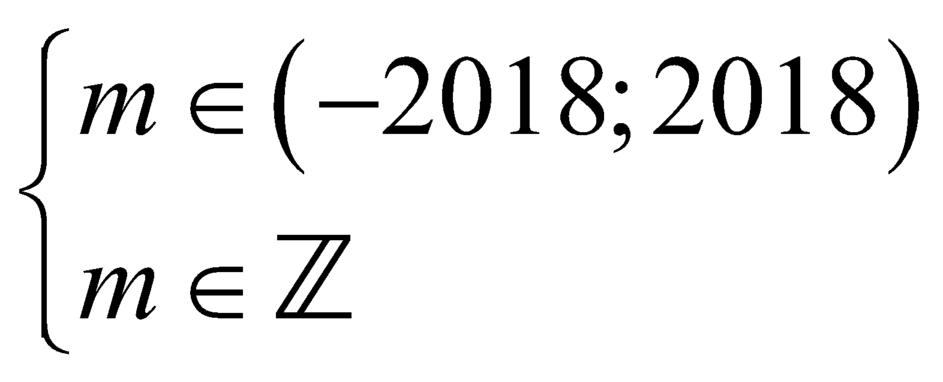4HDvlG6DqZiK.png

suy ra có NYyg1G3zVraD.png giá trị nguyên của hCAhjgdnNyXI.png thỏa mãn yêu cầu bài toán.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP