Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
n Ω = C 40 3
A : ‘ 3 sản phẩm lấy ra có ít nhất 1 sản phẩm tốt ‘
A ¯ : ‘3 sản phẩm lấy ra không có sản phẩm tốt ‘
n A ¯ = C 10 3 P ( A ) = 1 − P ( A ¯ ) = 1 − C 10 3 C 40 3 = 244 247
Chọn D
Ta có: 
Gọi A là biến cố lấy ra 3 sản phẩm trong đó có ít nhất một sản phẩm tốt.
=>
A
¯
là biến cố lấy ra 3 sản phẩm không có sản phẩm tốt và 
Vậy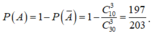 
Đáp án B
Gọi A là biến cố: “ 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”
Khi đó 
là biến cố :”3 sản phẩm lấy ra không có sản phẩm nào tốt”
Ta có:
Suy ra 
Đáp án B
Gọi A là biến cố: “ 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”
Khi đó A ¯ là biến cố :”3 sản phẩm lấy ra không có sản phẩm nào tốt”
Ta có:
Ω = C 10 3 ; Ω A = C 10 3 ⇒ P A ¯ = C 10 3 C 30 3 = 6 203
Suy ra
P A = 1 − P A ¯ = 197 203 .
Đáp án A
Lô 1 : Xác suất lấy sản phẩm tốt : 0,6
Xác suất lấy sản phẩm không tốt : 0,4
Lô 2 : Xác suất lấy sản phẩm tốt :0,7
Xác suất lấy sản phẩm không tốt : 0,3
⇒ xác suất để trong hai sản phẩm lấy ra có ít nhất một sản phẩm có chất lượng tốt :
p = 0 , 6.0 , 7 + 0 , 6.0 , 3 + 0 , 7.0 , 4 = 0 , 88
Chọn D
Số phần tử không gian mấu bằng số cách lấy ra 4 sản phẩm từ 20 sản phẩm là: C 20 4 (cách)
Cách 1: Để lấy ra 4 sản phẩm có sản phẩm lỗi ta chia các trường hợp:
TH1: Lấy được 3 sản phẩm tốt và 1 sản phẩm lỗi, ta có: C 18 3 . C 2 1 (cách)
TH2: Lấy được 2 sản phẩm tốt và 2 sản phẩm lỗi, ta có: C 18 2 . C 2 2 (cách)
Vậy xác suất cần tìm là: 
Cách 2: Xét biến cố đối:
Số cách lấy ra 4 sản phẩm không có sản phẩm lỗi C 18 4 (cách)
Vậy xác suất cần tìm là: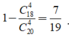 
Số phần tử của không gian mẫu: \(\left|\Omega\right|=C^6_{20}\)
a) Gọi A là biến cố: "Tất cả đều là chính phẩm."
Ta thấy \(\left|A\right|=C^6_{15}\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{ \left|\Omega\right|}=\dfrac{C^6_{15}}{C^6_{20}}=\dfrac{1001}{7752}\)
b) Gọi B là biến cố: "Tất cả đều là phế phẩm."
Rõ ràng \(\left|B\right|=0\) (vì chỉ có 5 phế phẩm nhưng ta chọn tới 6 sản phẩm nên không thể có chuyện cả 6 sản phẩm được chọn đều là phế phẩm) \(\Rightarrow P\left(B\right)=0\)
c) Gọi C là biến cố: "Có ít nhất 3 chính phẩm."
\(P_i\) là biến cố: "Có đúng \(i\) chính phẩm." \(\left(3\le i\le6\right)\)
Do \(P_i\) đôi một rời nhau và \(C=\cup^6_{i=3}P_i\) nên \(\left|C\right|=\sum\limits^6_{i=3}\left|P_i\right|\)
Ta thấy \(\left|P_i\right|=C^i_{15}.C^{6-i}_5\) \(\Rightarrow\sum\limits^6_{i=3}\left|P_i\right|=\sum\limits^6_{i=3}C^i_{15}.C^{6-i}_5=38220\)
hay \(\left|C\right|=38220\)
Từ đó \(P\left(C\right)=\dfrac{\left|C\right|}{\left|\Omega\right|}=\dfrac{38220}{C^6_{20}}=\dfrac{637}{646}\)
Đáp án C
n ( Ω ) = C 40 3
A : “3 sản phẩm lấy ra có ít nhất 1 sản phẩm tốt”
A : “3 sản phẩm lấy ra không có sản phẩm tốt”