Cho hình chóp S . A B C D có đáy là hình thoi tâm O cạnh a, A B C ^ = 60 ∘ , S A = S B = S C = 2 a . Tính khoảng cách giữa AB và SC.
A. a 11 8
B. 3 a 11 4
C. a 11 12
D. a 11 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)

Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(\Rightarrow\) CH là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCH}=60^0\)
Do \(\widehat{ABD}=60^0\Rightarrow\) các tam giác ABD và BCD là tam giác đều cạnh a
\(\Rightarrow\widehat{ABC}=120^0\)
Áp dụng định lý hàm cos cho tam giác BCH:
\(CH=\sqrt{BC^2+BH^2-2BC.BH.cos120^0}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow SH=CH.tan60^0=\dfrac{a\sqrt{21}}{2}\)
\(V=\dfrac{1}{3}SH.2S_{ABD}=\dfrac{1}{3}.\dfrac{a\sqrt{21}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{7}}{8}\)

Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?

Đáp án B
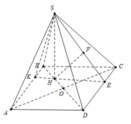
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14

Đáp án là A.

d B ; S C D = 3 2 d G ; S C D
Tính được: G H = a 3 3 ; S G = a 2 ; G K = a 7 .
Vậy d B ; S C D = 3 2 d G ; S C D = 3 2 . a 7 = 3 a 2 7 .

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Từ giả thiết suy ra: hình chóp S.ABC là hình chóp đều.
Gọi G là trọng tâm tam giác A B C ⇒ S G ⊥ A B C D
A B / / C D ⇒ A B / / S C D ⇒ d A B ; S C = d A B ; S C D = d B ; S C D = 3 2 d G ; S C D
(Vì B D G D = 3 2 ).
Trong mp (ABCD) vẽ G C ⊥ C D , C D ⊥ S G ⇒ C D ⊥ S G C ⇒ S G C ⊥ S C D
Mà S G C ∩ S C D = S C , vẽ G H ⊥ S C ⇒ d G ; S C D = G H
G B = G C = 2 3 . a 3 2 = a 3 3 .
⇒ S G = S B 2 − B G 2 = 4 a 2 − a 2 3 = a 11 3
Tam giác SHG vuông tại G:
1 G H 2 = 1 S G 2 + 1 G C 2 = 3 11 a 2 + 3 a 2 = 36 11 a 2 ⇒ G H = a 11 6
Vậy d A B ; S C = a 11 4