Một viên đạn khối lượng 50 g đang bay ngang với vận tốc không đổi 200 m/s tới đâm xuyên vào một tấm gỗ. Xét hai trường hợp : Viên đạn chui sâu 4 cm vào tấm gỗ dày và nằm yên trong đó. Xác định lực cản trung bình của gỗ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
28 tháng 11 2017
Áp dụng công thức về độ biến thiên động năng
m v 2 /2 - m v 0 2 /2 = A = - F c s
Trong đó F c là lực cản và s là độ xuyên sâu của viên đạn vào gỗ.
Khi viên đạn xuyên qua tấm gỗ dày s’ = 2 cm và bay ra ngoài, ta tìm được vận tốc của viên đạn khi vừa bay ra khỏi tấm gỗ (với lực cản của gỗ F c không đổi) :
6 tháng 3 2022
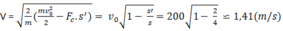
Câu 14.
a)Viên đạn dừng lại trước gỗ, công cản của nó:
\(A=-F\cdot s=\dfrac{1}{2}mv^2_2-\dfrac{1}{2}mv_1^2=-\dfrac{1}{2}mv^2_1\)
\(\Rightarrow F=\dfrac{mv^2_1}{2s}=\dfrac{0,04\cdot150^2}{2\cdot0,03}=15000N\)
b)Khi viên đạn xuyên qua tấm gỗ, độ biến thiên thế năng:
\(A'_c=-F_c'\cdot s=\dfrac{1}{2}mv_2'^2-\dfrac{1}{2}mv_1^2\)
\(\Rightarrow-15000\cdot0,01=\dfrac{1}{2}\cdot0,04\cdot v'^2_2-\dfrac{1}{2}\cdot0,04\cdot150^2\)
\(\Rightarrow v_2'=50\sqrt{6}\)m/s
6 tháng 3 2022
Câu 18.
Cơ năng ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot0^2+m\cdot10\cdot20=200m\left(J\right)\)
a)Cơ năng tai nơi vật chạm đất: \(W_1=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow200m=\dfrac{1}{2}mv^2\Rightarrow v=20\)m/s
b)Cơ năng vật tại nơi cách đất 10m là:
\(W_2=\dfrac{1}{2}mv_1^2+mgz'=\dfrac{1}{2}\cdot m\cdot v_1^2+m\cdot10\cdot10\left(J\right)\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow200m=\dfrac{1}{2}mv_1^2+m\cdot10\cdot10\)
\(\Rightarrow200=\dfrac{1}{2}v_1^2+100\Rightarrow v_1=10\sqrt{2}\)m/s
c)Cơ năng tại nơi \(W_đ=W_t\):
\(W_3=W_đ+W_t=2W_đ=2\cdot\dfrac{1}{2}mv_2^2=mv_2^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow200m=mv_2^2\Rightarrow v_2=10\sqrt{2}\)m/s
SS
22 tháng 2 2016
Năng lượng của viên đạn là: \(\frac{1}{2}mv^2=1000J\)
a. Để vật dừng lại trong gỗ thì năng lượng của vật chuyển hóa hoàn toàn thành công của lực cản:
\(F_c.S_1=E\Rightarrow F_c=250N\)
b.Công của lực cản chính là độ biến thiên năng lượng:
\(\frac{1}{2}mv^2-\frac{1}{2}mv'^2=F_c.S_2\)\(\Rightarrow v'=100\sqrt{2}m\text{/}s\)
DQ
22 tháng 1 2021
Độ biến thiên động năng của viên đạn bằng công của lực cản:
\(\dfrac{1}{2}mv-\dfrac{1}{2}mv_0^2=-F_c.s\)
Khi viên đạn xuyên vào gỗ nó dừng lại thì \(v=0\)
\(\Rightarrow-\dfrac{1}{2}mv_0^2=-F_c.s\)
\(\Rightarrow F_c=\dfrac{mv_0^2}{2s}=\dfrac{0,05.200^2}{2.0,04}=25000\) (N)
Nếu viên đạn xuyên qua tấm gỗ dày 2 cm chui ra ngoài thì ta có
\(\dfrac{1}{2}mv'^2-\dfrac{1}{2}mv_0^2=-F_c.s'\)
\(\Rightarrow v'=\sqrt{\dfrac{2}{m}\left(\dfrac{1}{2}mv_0^2-F_c.s'\right)}=\sqrt{v_0^2-\dfrac{2F_c.s'}{m}}=\sqrt{200^2-\dfrac{2.25000.0,02}{0,05}0^2}\approx141\) (m/s)
VT
25 tháng 11 2018
Đáp án D
Ta có:
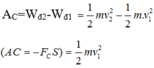
là công thức của lực cản của tấm gỗ: v 2 = 0 ; (dừng lại); v 1 = 200 (m/s)
Do đó:
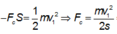
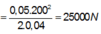
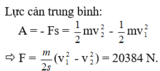
Áp dụng công thức về độ biến thiên động năng
m v 2 /2 - m v 0 2 /2 = A = - F c s
Trong đó F c là lực cản và s là độ xuyên sâu của viên đạn vào gỗ.
Khi viên đạn xuyên vào và nằm trong tấm gỗ (v = 0), ta tìm được lực cản của gỗ:
F c = m v 0 2 /2s = (50. 10 - 3 . 200 2 )/(2.4. 10 - 2 ) = 25000(N)