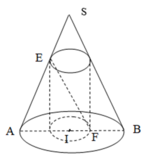
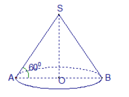
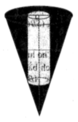
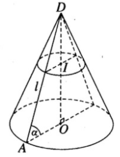
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng.
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β

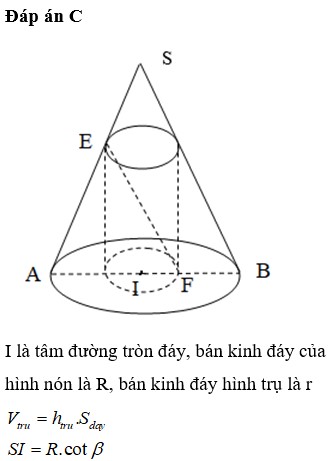

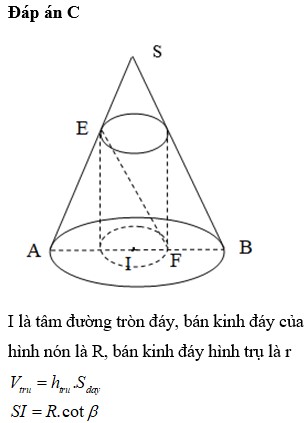
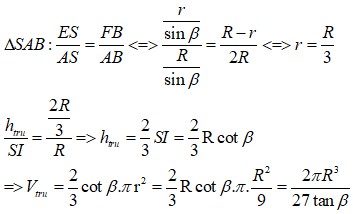
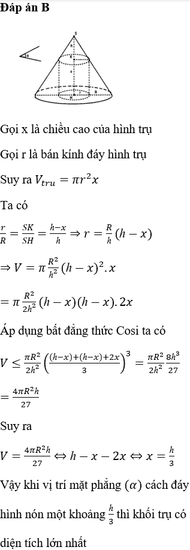
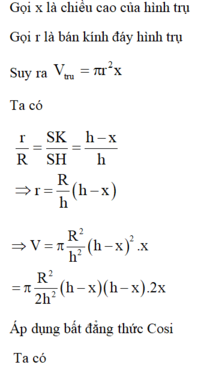
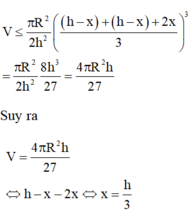


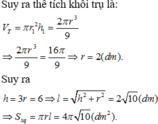
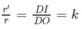
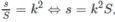
Đáp án C
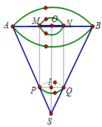
I là tâm đường tròn đáy, bán kinh đáy của hình nón là R, bán kinh đáy hình trụ là r
V t r u = h t r u . S d a y
S I = R . c o t β
⇔ r = R 3
h t r u S I = 2 R 3 R ⇒ h t r u = 2 3 S I = 2 3 R . c o t β
⇒ V t r u = 2 3 c o t β . π . r 2 = 2 πR 3 27 tanβ