giúp mình với ạ, cần gấp1) Cho tam giác ABC có trung tuyến AI. Trên AI lấy điểm G bất kì, BG cắt AC tại E, CG cắt AB tại F. Chứng minh rằng: EF // BC.2) Cho tam giác ABC có M là trung điểm của BC, điểm N nằm trên cạnh AB sao cho AN = 1/3AB, điểm Q nằm trên cạnh AC sao cho AQ = 2/3 AC, đường thẳng QN cắt đường thẳng AM và BC lần lượt tại điểm P, R.a) Tính: RB/RC,PA/PM ?b) Đường thẳng đi qua N song song với BC cắt...
Đọc tiếp
giúp mình với ạ, cần gấp
1) Cho tam giác ABC có trung tuyến AI. Trên AI lấy điểm G bất kì, BG cắt AC tại E, CG cắt AB tại F. Chứng minh rằng: EF // BC.
2) Cho tam giác ABC có M là trung điểm của BC, điểm N nằm trên cạnh AB sao cho AN = 1/3AB, điểm Q nằm trên cạnh AC sao cho AQ = 2/3 AC, đường thẳng QN cắt đường thẳng AM và BC lần lượt tại điểm P, R.
a) Tính: RB/RC,PA/PM ?
b) Đường thẳng đi qua N song song với BC cắt AC tại T. Chứng minh rằng: CN, BT cắt nhau tại trung điểm của AM.
3) Cho tam giác ABC có trung tuyến AI và trọng tâm G. Qua G dựng đường thẳng d bất kì cắt các cạnh AB, AC lần lượt tại M, N.
a) Chứng minh rằng: AB/AM + AC/AN có giá trị không đổi khi (d) thay đổi.
b) Xác định vị trí của đường thẳng (d) để AM/AB+AN/AC đạt GTNN.
4) Cho tam giác ABC ,một đường thẳng thay đổi cắt các cạnh AB, AC tại E, F sao cho: AB/AE+AC/FA=4 . Chứng minh rằng EF luôn đi qua một điểm cố định.
5) Cho tam giác nhọn ABC và điểm D bất kì trên cạnh BC, lấy một điểm E thuộc đoạn AD, F thuộc đoạn DE. Một đường thẳng qua F song song với BC cắt AB, EB, EC, AC theo thứ tự tại M, P, Q, N. Đường thẳng MD và EB cắt nhau tại R, ND và EC cắt nhau tại S, DP và AB cắt nhau tại G, DQ và AC cắt nhau tại H. Chứng minh rằng:
a) MP/BD=NQ/DC
b) RS // BC
c) GH // RS
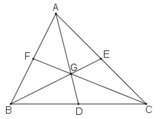


Trên đường trung tuyến AD có điểm G thỏa mãn: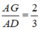
Suy ra: G là trọng tâm tam giác ABC.
Do tia BG cắt AC tại E nên E là trung điểm của AC.
Do tia CG cắt AB tại F nên F là trung điểm của AB.
Theo tính chất trọng tâm tam giác ta có:
Chọn (B)