Cho khối chóp S.ABCD có M ∈ SA, N ∈ SB cho M A → = - 2 M S → , N S → = - 2 N B → . Mặt phẳng ( α ) đi qua hai điểm M, N và song song với SC chia khối chóp thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó (số bé chia số lớn).
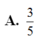
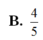
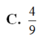
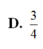
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
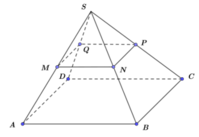
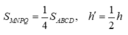
(với h’ và h lần lượt là khoảng cách từ S đến (MNPQ) và (ABCD)).
![]()
=> Chọn phương án A.

Theo công thức Simsons ta có:
\(\dfrac{V_{SMNPQ}}{V_{SABCD}}=\dfrac{2V_{SMNP}}{2V_{SABC}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}.\dfrac{SP}{SC}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{8}\)

Đáp án D
Hướng dẫn giải:
Ta có S A B C = a 2 2 , S A = S B 2 - A B 2 = a 3
V S . A B C = 1 3 S A . S A B C = 1 3 a 3 . a 2 2 = a 3 3 6
Ta lại có V B . N A M V B . C A S = B N B C . B M B S = 1 4
⇒ V B . N A M = 1 4 V B . C A S
Kết luận V A . S C N M = V S . A B C - V B . N A M = a 3 3 8

Đáp án D
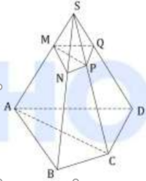

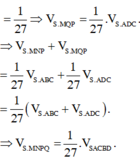
Chú ý: Em nhớ rằng, công thức tính tỉ số thể tích chỉ áp dụng cho khối chóp tam giác. Còn với khối chóp tứ giác, ngũ giác, lục giác,… em cần chia ra thành các khối chóp tam giác và áp dụng công thức.
Công thức giải nhanh:
Cắt khối chóp bởi mặt phẳng song song với đáy: Xét khối chóp S . A 1 A 2 . . . . . A n , mặt phẳng (P) song song với mặt đáy cắt cạnh S A 1 tại m thỏa mãn . Khi đó (P) chia khối chóp thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V' và khối đa diện ban đầu có thể tích V thì V ' V = k 3
Nên ⇒ V S . M N P Q V S . A B C D = 1 3 2 = 1 27
Đáp án B