Góc ADB trên hình bs 3 có số đo bằng
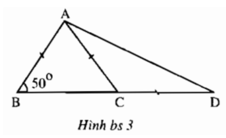
(A) 20o;
(B) 25o;
(C) 30o;
(D) 35o;
Hãy chọn phương án đúng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 8 2019
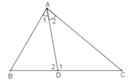
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o
CC
0
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
a, Các góc có trong hình vẽ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB} ; \widehat{BDA} ; \widehat{DAB} ; \widehat{ABD} ; \widehat{DBC} ; \widehat{DAC}\)
Những góc có số đo bằng 60 độ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB}\)
b, Điểm D có nằm trong góc ABC. Điểm C không nằm trong góc ADB.
c, Số đo góc ABD là: 40o.
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2022
\(BD=a\sqrt{2}\)
\(\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=\widehat{SBD}=\dfrac{SB^2+BD^2-SD^2}{2SB.BD}=\dfrac{a^2+2a^2-a^2}{2a.a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=45^0\)
DN
8 tháng 3 2022
thầy ơi bưa trước thầy em có giảng cái cách mà SB=SD thì suy ra SBD là nửa hình vuông nên góc SBD 45 độ v đúng ko thầy?
CT
24 tháng 1 2019
góc ACB=(180 độ -40 độ)/2=70 độ
suy ra góc BCD=180 độ -70 độ =110 độ
do CB=CD nên tam giác BCD cân tại C
suy ra góc CDB=(180 độ -110 độ)/2=35 độ
hay góc ADB =35 độ
+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A
+) Tam giác ACD có góc ACB là góc ngoài của tam giác nên:
+) Lại có: AC = CD ( giả thiết) nên tam giác ACD cân tại C.
Chọn đáp án B