Cc ho tam giáABC có: ∠B - ∠C = 20o. Tia phân giác của góc A cắt BC tại D. tính số đo các góc ∠(ADC) , ∠(ADB)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
1
24 tháng 12 2021
Xét tam giác ABC: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}\)
Mặt khác: \(\widehat{B}-\widehat{C}=18^0\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\dfrac{180^0-\widehat{A}+18^0}{2}=99^0-\dfrac{\widehat{A}}{2}\\\widehat{C}=99^0+\dfrac{\widehat{A}}{2}-18^0=81^0-\dfrac{\widehat{A}}{2}\end{matrix}\right.\)
Xét tam giác ABD: \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=\dfrac{\widehat{A}}{2}+99^0-\dfrac{\widehat{A}}{2}=99^0\)
\(\widehat{ABD}=180^0-\widehat{ADC}=81^0\)
2
21 tháng 4 2021
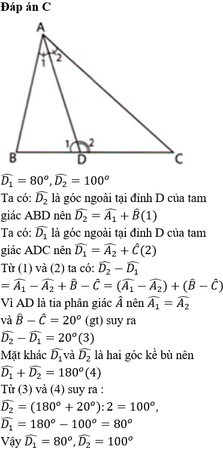
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o
21 tháng 2 2022
Đặt \(\widehat{ADC}=b;\widehat{ADB}=a\)
Ta có: \(a+\widehat{B}+\widehat{BAD}=b+\widehat{C}+\widehat{CAD}\)
\(\Leftrightarrow a+\widehat{C}+20^0=b+\widehat{C}\)
\(\Leftrightarrow a-b=-20\)
mà a+b=180
nên 2a=160
=>a=80
=>b=100
LA
3
22 tháng 11 2016
Ta có:B-C=20
Ta lại có: BAD=DAC( tính chất tia phân giác).
Do:ADC=BAD+ABD( tính chất góc ngoài)
ADB=DAC+ACD( tính chất góc ngoài)
→ADC-ADB= B-C=20→ADC=ADB+20 (1).
Lại do ADC+ADB=180 (2)
Thay (1) vào (2) ta được:
20+ADB+ADB=180
→ 20+2ADB= 180
→ 2ADB=160
→ ADB=80 (3)
Thay (3) vào (1) ta được:
ADC=80+20
→ ADC=100
18 tháng 12 2019
Vì ADB là goc là góc ngoài của ∆ADC
Suy ra góc ADB =góc DAC+C mà AD là phân giác góc A
Suy ra ADB=C+A/2 (1)
Vì ADC là góc ngoài của_∆ADB
Suy ra ADC=BAD+
Mà Ad là phân giác cẩu
Suy ra ADC=B+A/2 (2)
Từ 1 và 2 suy ra B-C =ADC-ADB=20
Mà ADC+ ADB =180(kề bù)
Suy ra ADC=(180+20)/2=100
Suy ra ADB=180-100=80
Vậy ADB =80
Vậy ADC=100
8 tháng 12 2018
Bài làm
a) Xét tam giác ABC
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( định lí tổng ba góc của tam giác )
hay 80o + 45o + \(\widehat{C}\)= 180o
=> \(\widehat{C}\)= 180o - 80o - 45o
=> \(\widehat{C}\)= 55o
Vậy \(\widehat{C}\)= = 55o
b) Gọi \(\widehat{ACx}\)là góc ngoài của tam giác ABC tại đỉnh C
Ta có: \(\widehat{ACx}=\widehat{A}+\widehat{B}\)( tính chất góc ngoài của tam giác )
hay\(\widehat{ACx}\) = 80o + 45o
=> \(\widehat{ACx}\) = 125o
Vậy \(\widehat{ACx}\)= 125o
c) Vì AD là tia phân giác của \(\widehat{BAC}\)
=> \(\widehat{BAD}\)= \(\widehat{\frac{BAC}{2}}=\frac{80^0}{2}=40^0\)
Xét tam giác ABD
Ta có:\(\widehat{ADB}\)= \(\widehat{BAD}\)+ \(\widehat{ABD}\)+ \(\widehat{ADB}\)= 180o( định lí tổng ba góc của tam giác )
hay \(40^0+45^0+\text{}\text{}\widehat{ADB}=180^0\)
=> \(\widehat{ADB}=180^0-40^0+45^0\)
=>\(\widehat{ADB}=85^0\)
Vậy \(\widehat{ADB}=85^0\)
Vì \(\widehat{ADC}\)là góc ngoài của tam giác ABD tại đỉnh D
Ta có: \(\widehat{ADC}\)= \(\widehat{ADB}+\widehat{ABD}\)
hay \(\widehat{ADC}\)= \(40^0+45^0\)
=> \(\widehat{ADC}\)= \(85^0\)
Vậy \(\widehat{ADC}\)= \(85^0\)
# Chúc bạn học tốt #
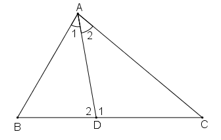
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o