Tìm tập xác định D của hàm số y = log x - 2 1 - x
A. D = - ∞ ; 1 ∪ 2 ; + ∞
B. D = 1 ; 2
C. D = ℝ \ 1
D. D = ℝ \ 1 ; 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 5 2018
Chọn A
Điều kiện xác định:
Vậy tập xác định của hàm số (1) là 
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
a, Điều kiện: \(2^x\ne3\Rightarrow x\ne log_23\)
Vậy D = R \ \(log_23\)
b, Điều kiện: \(25-5^x\ge0\Rightarrow5^x\le5^2\Rightarrow x\le2\)
Vậy D = \((-\infty;2]\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
c, Điều kiện: \(\left\{{}\begin{matrix}x>0\\lnx\ne1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\x\ne e\end{matrix}\right.\)
Vậy D = \(\left(0;+\infty\right)\backslash\left\{e\right\}\)
d, Điều kiện: \(\left\{{}\begin{matrix}x>0\\1-log_3x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\log_3x\le1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\x\le3\end{matrix}\right.\Rightarrow0< x\le3\)
Vậy D = \((0;3]\)
15 tháng 8 2023
Chọn D. Bởi vì hàm số ln x luôn luôn dương nên chắc chắn sẽ đồng biến trên TXĐ của nó
CM
31 tháng 8 2018
Chọn B
Xét hàm số y = -log(2x- x 2 )
Điều kiện xác định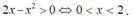 
Tập xác định D = (0;2)
Đáp án B
Điều kiện x - 2 1 - x > 0 ⇔ 1 < x < 2