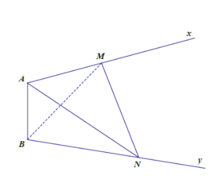
Cho đoạn thẳng AB cố định trong không gian và có độ dài AB = 2. Qua các điểm A và B lần lượt kẻ các đường thẳng Ax và By chéo nhau thay đổi nhưng luôn vuông góc với đoạn thẳng AB. Trên các đường thẳng đó lần lượt lấy các điểm M N, sao cho AM+2BN=3. Tìm giá trị lớn nhất của thể tích khối tứ diện ABMN ?


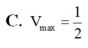
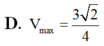



Đáp án B