Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = x 2 + m 4 - x 2 + m - 7 có điểm chung với trục hoành là [a;b] (với a;b ∈ ℝ ). Tính giá trị của S = 2a + b.
A. S = 19 3
B. S = 7
C. S = 5
D. S = 23 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4

Lời giải:
Đồ thị hàm số \(y=-x^4+2(m+2)x^2-(4+m)\) không có điểm chung với trục hoành nghĩa là phương trình \(x^4-2(m+2)x^2+(m+4)= 0\) vô nghiệm
Đặt \(x^2=t\). Khi đó ta cần tìm $m$ nguyên sao cho \(t^2-2(m+2)t+(m+4)=0(1)\) vô nghiệm
Sẽ có hai kiểu xảy ra:
Kiểu 1: \((1)\) có \(\Delta'=(m+2)^2-(m+4)=m^2+3m<0\Leftrightarrow -3< m<0\)
Vì \(m\in\mathbb{Z}\Rightarrow m\in \left \{ -1,-2 \right \}\)
Kiểu 2: \((1)\) có nghiệm nhưng hai nghiệm đó là hai nghiệm âm( Kết hợp với \(t\geq 0\) sẽ suy ra mâu thuẫn, phương trình vô nghiệm)
Trước tiên \(\Delta'=m^2+3m\geq 0\Rightarrow \) \(\left[\begin{matrix}m\ge0\\m\le-3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{\begin{matrix} t_1+t_2=2(m+2)<0 \\ t_1t_2=m+4> 0\end{matrix}\right.\Rightarrow -4< m<-2\Rightarrow m=-3\)
Vậy \(m\in \left \{-1,-2,-3\right\}\)

Đáp án C
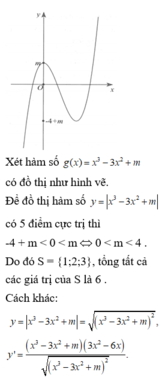
Đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 5 nghiệm phân biệt và y’ đổi dấu qua 5 nghiệm đó, điều này tương đương với x 3 - 3 x 2 + m có ba nghiệm phân biệt khác 0 và 2

Đáp án là B.
• Trường hợp m = 0
f x = − x 2 + 1 có đồ thị là parabol, có đỉnh I(0;-1).
Đồ thị hàm số đã cho có một điểm cực đại là I thuộc trục tung.
Do đó m = 0 thoả yêu cầu bài toán.
• Trường hợp m ≠ 0
f ' x = 4 m x 3 − 2 m + 1 x
f ' x = 0 ⇔ x = 0 ∨ x 2 = m + 1 2 m
+ Nếu − 1 ≤ m < 0 thì f ' ( x ) = 0 có nghiệm x = 0 ( y = m + 1 )

Đồ thị hàm số có một điểm cực đại (0;m+1) thuộc trục toạ độ.
+ Nếu m < − 1 ∨ m > 0 thì f ' ( x ) = 0 có ba nghiệm phân biệt
x = 0 y = m + 1 x = m + 1 2 m ( y = 3 m 2 + 2 m − 1 4 m ) x = − m + 1 2 m ( y = 3 m 2 + 2 m − 1 4 m )
Khi đó đồ thị hàm số có các điểm cực trị thuộc các trục toạ độ khi và chỉ khi 3 m 2 + 2 m − 1 = 0 ⇔ m = − 1 ∨ m = 1 3 . Nhận m = 1 3
Đáp án đúng : B