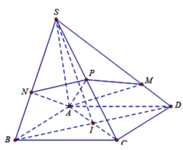
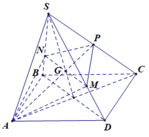
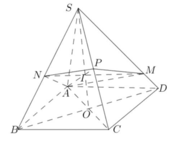
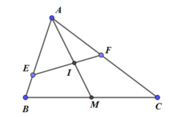
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V 1 là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của V 1 V ?
A. 1 8
B. 2 3
C. 3 8
D. 1 3

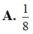
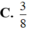
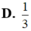
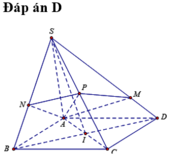



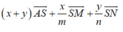
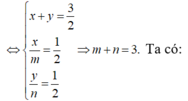
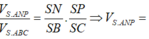

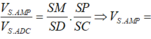
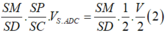

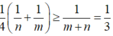
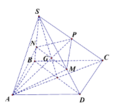
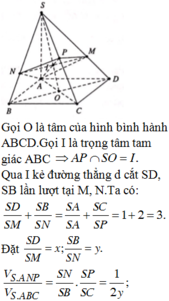
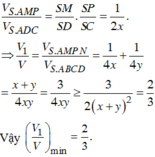
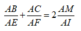
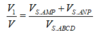
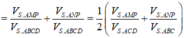

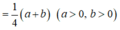
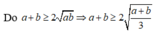
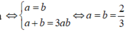
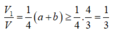

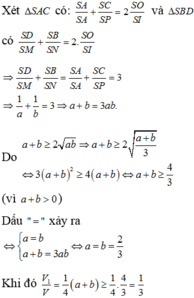
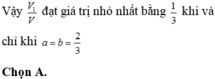

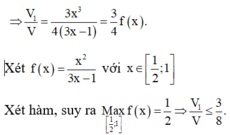

Đáp án D