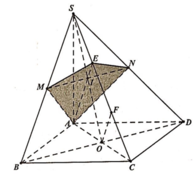
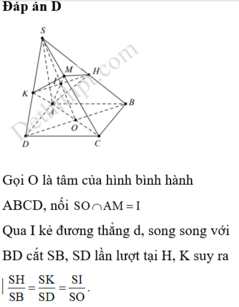
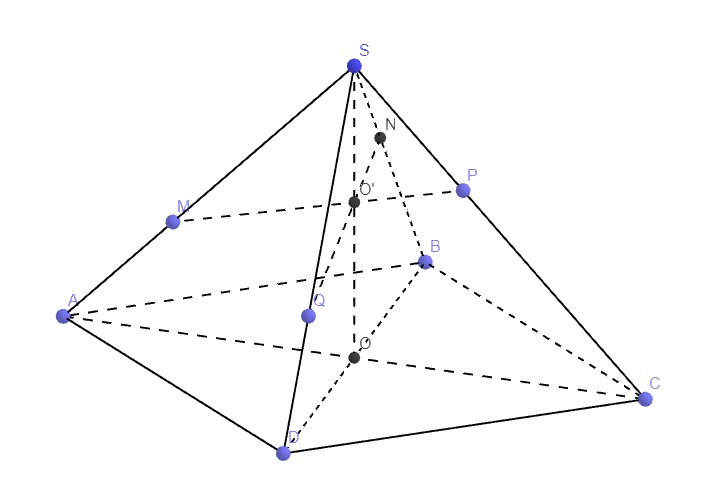
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là điểm di động trên cạnh SC (M không trùng S và C), mặt phẳng (α) chứa đường thẳng AM song song với BD lần lượt cắt các cạnh SB, SD tại E và F. Giá trị T = S B S E + S D S F - S C S M bằng
A. 1
B. 2
C. 1 2
D. 3 2

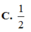
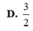

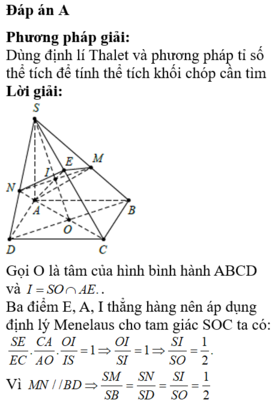
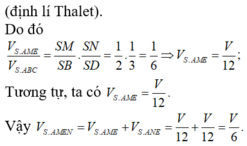

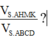




Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.