Cho hình chóp S.ABCD có
S
A
⊥
A
B
C
D
,
A
C
=
a
2
,
S
A
B
C
D
=
3
a
2
2
và góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
60
0
.
Gọi H là hình chiếu vuông góc của A trên SC. Tính theo a thể tích khối chóp H.ABCD. A.
a
3
6
2
.
B.
a
3
...
Đọc tiếp
Cho hình chóp S.ABCD có S A ⊥ A B C D , A C = a 2 , S A B C D = 3 a 2 2 và góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 60 0 . Gọi H là hình chiếu vuông góc của A trên SC. Tính theo a thể tích khối chóp H.ABCD.
A. a 3 6 2 .
B. a 3 6 4 .
C. a 3 6 8 .
D. 3 a 3 6 4 .
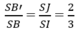
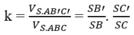
Đáp án C.
Do:
S C ; A B C ^ = 60 0 ⇒ S C A ^ = 60 0 ⇒ S A = A C tan 60 0 = a 6
Ta có: Δ S A C vuông tại A có đường cao AH.
Khi đó:
S A 2 = S H . S C ⇒ S A 2 S C 2 = S H S C = 6 a 2 6 a 2 + 2 a 2 = 3 4 ⇒ H C S C = 1 4 .
Do đó:
d H ; A B C D = 1 4 d C ; A B C D ⇒ V H . A B C D = 3 4 V S . A B C D = 1 4 . 1 3 . a 6 . 3 a 2 2 = a 2 6 8 .