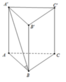
Cho lăng trụ đứng ABC.A’B’ C’ có đáy là tam giác vuông tại A,AC = a và A C B ^ = 60 0 ; góc giữa BC’ và (AA’C) bằng 30 0 . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = a 3 6
B. V = 2 a 3 6
C. V = a 3 3 6
D. V = a 3 6 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
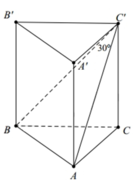
Ta có B A ⊥ AA ' B A ⊥ AC ⇒ B A ⊥ A C C ' A '
Do đó góc giữa BC’ và (AA’C) bằng A C ' A ^ = 30 0
Khi đó A C ' tan 30 0 = A B ⇒ A C ' = A B tan 30 0
Mặt khác A B = A C tan C = a 3 ⇒ A C ' = 3 a .
⇒ C C ' = A C ' 2 − A C 2 = 2 a 2 ⇒ V = S A B C . C C ' = A B . A C 2 . C C ' = a 3 6.

Chọn A.
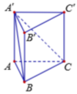
Do đáy tam giác vuông cân tại B, AC = a 2 nên AB = a.
Lại có: ![]() nên góc tạo bởi (A'BC) và đáy là
A
'
B
A
^
nên góc tạo bởi (A'BC) và đáy là
A
'
B
A
^
Theo bài ra: A ' B A ^ = 60 °
![]()
Thể tích V của khối lăng trụ: ![]()

Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:

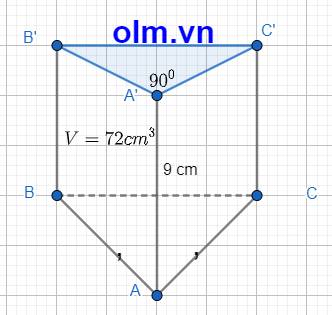
VABCA'B'C' = SABC.h
Diện tích của tam giác ABC là: 72 : 9 = 8 (cm2)
SABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB2 = 8 ⇒ AB2 = 8.2 = 16
⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)
Vậy độ dài cạnh đáy AB dài 4cm

Đáp án B
Ta có: A A ' ⊥ A B C ⇒ A ' B A ⏜ = A ' B ; A B C ^ = 60 ∘
Do đó A A ' = A B tan 60 ∘ = a 15 ; S A B C = A B 2 2 = 5 a 2 2
Suy ra V A B C . A ' B ' C ' = S h = 5 a 2 2 . a 15 = 5 a 3 15 2 .