Điền vào chỗ trống cụm từ nào cho dưới đây để được một mệnh đề đúng?
“Tâm các mặt của một hình lập phương là các đỉnh của một….”
A. Hình 12 mặt đều
B. Hình bát diện đều
C. Hình lập phương
D. Hình tứ diện đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
“Trung điểm các cạnh của hình tứ diện đều là các đỉnh của một hình bát diện đều”.

Đáp án C
“Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều. Đó chính là khối mười hai mặt đều”.

Đáp án là D
“Số cạnh của một hình đa diện luôn lớn hơn số mặt của hình đa diện ấy.”

Đáp án là D
“Số cạnh của một hình đa diện luôn lớn hơn số mặt của hình đa diện ấy.”

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là 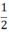 . 4.6 = 12 cm2.
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là 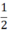 . 4.6 = 12 cm2.
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.

1)
Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', Phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABA', A'ABD', A'B'BD' bằng nhau
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.

1)
Chia lăng trụ ABD.A’B’D’ thành ba tứ diện DABD’, A’ABD’, A’B’BD’. Phép đối xứng qua (ABD’) biến DABD’ thành A’ABD’, Phép đối xứng qua (BA’D’) biến A’ABD’ thành A’B’BD’ nên ba tứ diện DABA’, A’ABD’, A’B’BD’ bằng nhau.
Làm tương tự đối với lăng trụ BCD.B’C’D’ ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.
Đáp án B
“Tâm các mặt của một hình lập phương là các đỉnh của một hình bát diện đều”