Người ta dùng một thanh sắt tròn có độ dài ban đầu l 0 = 50 cm và tiết diện ngang S = 2,5 m m 2 . Kéo dãn thanh sắt bằng lực F có cường độ tăng dần và đo độ dãn dài ∆ l tương ứng của nó (Bảng 34-35. 1). Dựa vào đồ thị vẽ được, tìm giá trị của suất đàn hồi E và hệ số đàn hồi k.
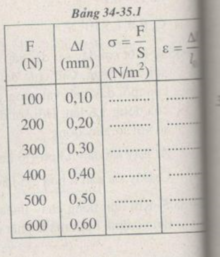

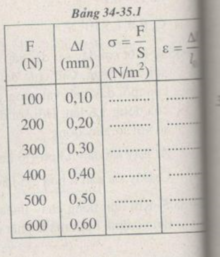
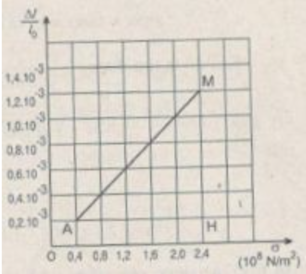
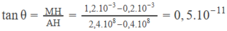
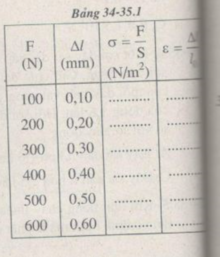
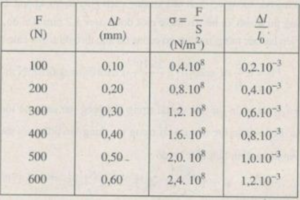
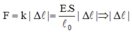
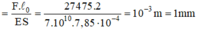
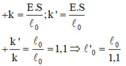
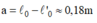



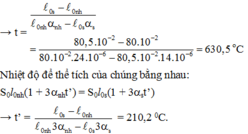
Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.
Từ đó tìm đươc suất đàn hồi :
và hệ số đàn hồi: