Cặp điểm thuộc đồ thị (C) của hàm số 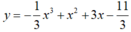 mà chúng đối xứng nhau qua trục tung là
mà chúng đối xứng nhau qua trục tung là
A.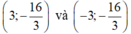
B. 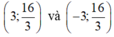
C. 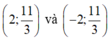
D. 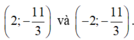
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi ![]()
là hai điểm trên (C) đối xứng nhau qua I(2;18).
Ta có:
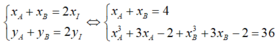
![]()
Thay (1) vào (2) ta được
![]()
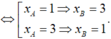 .
.
Vậy cặp điểm cần tìm là A(1;2);B(3;34).
Số cặp điểm thuộc đồ thị (C) của hàm số ![]() đối xứng với nhau qua điểm I(2;18) là
đối xứng với nhau qua điểm I(2;18) là
A. 2.
B. 1
C. 3.
D. 4.

Đáp án B
Gọi M(x;y) là điểm trên đồ thị (C), gọi N là điểm đối xứng với M qua I, ta có
![]() . Vì N thuộc (C), ta có
. Vì N thuộc (C), ta có
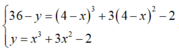
![]()
![]()
Vậy có tất cả một cặp điểm thuộc đồ thị (C) thỏa mãn yêu cầu đề bài.

Đáp án C
Gọi ![]()
![]() là hai điểm trên O đối xứng nhau qua gốc tọa độ.
là hai điểm trên O đối xứng nhau qua gốc tọa độ.
Ta có
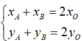
<=>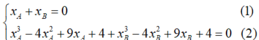
Thay (1) vào (2) ta được
![]()
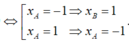
Vậy cặp điểm cần tìm là ![]()

Đáp án D
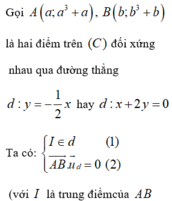


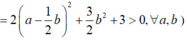
Với ![]()
, từ (2) ta có:
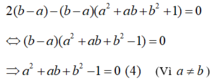
Thay (3) vào (4) ta được

Vậy cặp điểm cần tìm là
![]()

Đáp án B

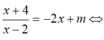
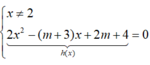
Điều kiện cần:
Để ∆ cắt (C) tại hai điểm phân biệt thì phương trình h(x) = 0 có hai nghiệm phân biệt khác 2, tức là
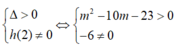
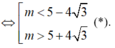
Điều kiện đủ:
Gọi I là trung điểm của AB, ta có:
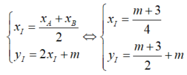
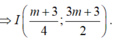

![]()
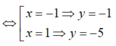
Vậy tọa hai điểm cần tìm là
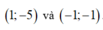

Đáp án A
Phương pháp: Tham số hóa điểm thuộc đồ thị hàm số (C).
Lấy điểm đối xứng với điểm đó qua O (Điểm (a;) đối xứng với điểm (-a;-b)qua gốc tọa độ O).
Cho điểm đối xứng vừa xác định thuộc (C).
Cách giải:
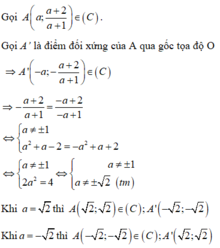
Chú ý và sai lầm : Có thể thử trực tiếp từng đáp án và suy ra kết quả.
Đáp án B
Phương pháp tự luận
Gọi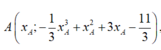
Ta có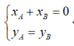
Thay (1) vào (2) ta được:
Vậy có hai cặp điểm cần tìm là
Phương pháp trắc nghiệm
Kiểm tra điều kiện đối xứng qua trục tung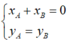
và kiểm tra điểm có thuộc đồ thị không.