Trên mặt phẳng tọa độ, hãy tìm tập hợp các điểm biểu diễn số phức z thỏa mãn từng bất đẳng thức: |z - i| ≤ 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 2 2019
z – 1 – i = (x – 1) + (y – 1)i
|z – 1 – i| < 1
⇔ x - 1 2 + y - 1 2 < 1 .
Vậy tập hợp các điểm cần tìm là hình tròn (không kể biên) tâm (1; 1), bán kính bằng 1.
CM
17 tháng 11 2018
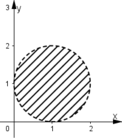
Tập hợp các điểm M(x; y) của mặt phẳng tọa độ biểu diễn số phức z = x + yi thỏa mãn điều kiện:
Các điểm M(x; y) như vậy nằm trong đường tròn có tâm O bán kính bằng 2 không kể các điểm trên đường tròn.
PT
1
CM
28 tháng 8 2018
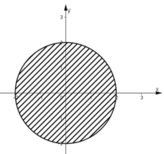
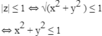
Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1.
PT
1
CM
16 tháng 12 2019
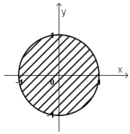
Gọi số phức z = x + y.i có điểm biểu diễn là M(x; y).
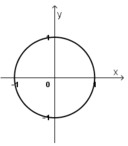
|z| = 1 ⇔ x 2 + y 2 = 1 ⇔ x 2 + y 2 =1
Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.
PT
1
CM
7 tháng 12 2018
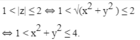
Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính đường tròn nhỏ bằng 1,đường tròn lớn bằng 2, không kể các điểm thuộc đường tròn nhỏ.
PT
1
CM
11 tháng 4 2017
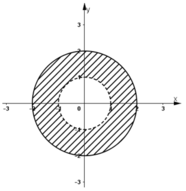
Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z 0 = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1) (H. 14)
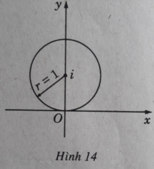
Ta có thể tiến hành như sau:
Cho z = x + iy, ta có | z - 1 | 2 = | x + y - 1 i | 2 = x 2 + y - 1 2 và như vậy ta có: x 2 + y - 1 2 = 1
Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)
CM
7 tháng 2 2017
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z1 được biểu diễn bởi điểm A(1;-1).
Em có: |z - 1 + i| = 2 => MA = 2
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: 
Cách 2: Đặt 
. Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
Vậ tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình: 
CM
20 tháng 5 2017
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z 1 được biểu diễn bởi điểm A(1;-1).
Em có: z − 1 + i = 2 ⇒ MA = 2 .
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: x − 1 2 + y + 1 2 = 4 .
Cách 2: Đặt z = x + yi , x ; y ∈ ℝ . Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
z − 1 + i = 2 ⇔ x − 1 + y + 1 i = 2 ⇔ x − 1 2 + y + 1 2 = 2 ⇔ x − 1 2 + y + 1 2 = 4
Vậy tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình:
x − 1 2 + y + 1 2 = 4 .
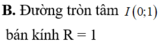
z – i = x + (y – 1).i
|z – i| ≤ 1
Tập hợp tất cả các điểm biểu diễn các số phức thỏa mãn |z – 1| ≤ 1 là các điểm của hình tròn tâm (0; 1) bán kính bằng 1 kể cả biên.